题目内容
对一切实数x,不等式 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A. | B. | C. | D.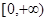 |
B
解析试题分析:根据题意,由于对一切实数x,不等式 恒成立,那么可知
恒成立,那么可知 恒成立,那么可知
恒成立,那么可知
,当|x|=1,时成立,
当x=0时,则a可以取一切实数,
因此可知a的范围是取交集得到为 ,故选B.
,故选B.
考点:本试题主要是考查了不等式的恒成立问题的运用。
点评:对于含有参数的不等式的恒成立问题,可以采用分离参数a的思想来得到其取值范围即可。如果直接法用二次函数比较麻烦些。这也是一种很好的等价转化方法之一,属于基础题。

练习册系列答案
相关题目
设a,b为满足ab<0的实数,那么 ( )
| A.|a+b|>|a-b| | B.|a+b|<|a-b| | C.|a-b|<|a|-|b| | D.|a-b|<|a|+|b| |
设 ,
, ,
, ,则它们的大小关系是
,则它们的大小关系是
A. | B. | C. | D.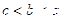 |
不等式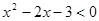 的解集为
的解集为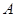 ,不等式
,不等式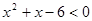 的解集为
的解集为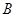 ,不等式
,不等式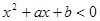 的解集是
的解集是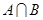 ,那么
,那么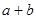 等于 ( )
等于 ( )
| A.-3 | B.1 | C.-1 | D.3 |
已知x>0,y>0,x+y+xy="2," 则x+y的最小值是
A.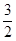 | B.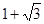 | C. | D. |
若不等式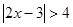 与不等式
与不等式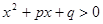 的解集相同,则p:q等于 ( )
的解集相同,则p:q等于 ( )
| A.12:7 | B.7:12 | C.-12:7 | D.-3 :4 |
在R上定义运算 若不等式
若不等式 对任意实数
对任意实数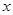 成立,则( )
成立,则( )
A. | B.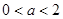 |
C.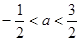 | D.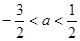 |
不等式 对任意实数
对任意实数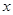 恒成立,则实数
恒成立,则实数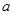 的取值范围为( )
的取值范围为( )
A. | B.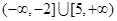 |
C. | D.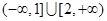 |
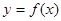 的图象是中心在原点,焦点在
的图象是中心在原点,焦点在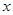 轴上的椭圆的两段弧,则不等式
轴上的椭圆的两段弧,则不等式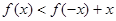 的解集为 ( )
的解集为 ( )