题目内容
如图,函数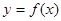 的图象是中心在原点,焦点在
的图象是中心在原点,焦点在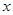 轴上的椭圆的两段弧,则不等式
轴上的椭圆的两段弧,则不等式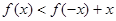 的解集为 ( )
的解集为 ( )
A. |
B. |
C. |
D.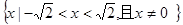 |
A
解析试题分析:由图像知f(x)为奇函数,所以f(-x)=-f(x).所以原不等式可化为f(x)< ,
,
由图像易知,包含这两段弧的椭圆方程为  ,
,
与直线y= 联立得
联立得  ,
,
结合图像知:不等式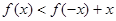 的解集为
的解集为 。
。
考点:函数的奇偶性;
点评:本题主要考查奇函数的性质和椭圆的标准方程,体现了数形结合及转化的数学思想.根据已知条件对不等式进行转化变形是解答本题的关键.

练习册系列答案
相关题目
不等式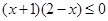 的解集为( )
的解集为( )
A.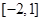 | B.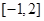 |
C.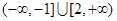 | D.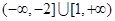 |
若方程 在(0,1)内恰有一解,则a的取值范围是( )
在(0,1)内恰有一解,则a的取值范围是( )
A. | B.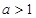 | C. | D. |
对一切实数x,不等式 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A. | B. | C. | D.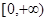 |
定义: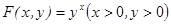 ,已知数列
,已知数列 满足
满足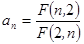
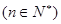 ,若对任意正整数
,若对任意正整数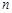 ,都有
,都有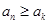
 成立,则
成立,则 的值为 ( )
的值为 ( )
| A.2 | B.1 | C.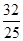 | D.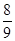 |
若不等式 成立的充分条件是
成立的充分条件是 ,则实数
,则实数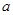 的取值范围是( )
的取值范围是( )
A.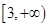 | B. | C. | D.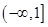 |
设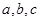 均为正数,且
均为正数,且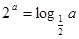 ,
,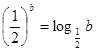 ,
,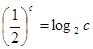 则( )
则( )
A. | B.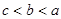 | C.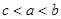 | D.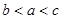 |
不等式 对于
对于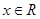 恒成立,那么
恒成立,那么 的取值范围是( )
的取值范围是( )
A. | B.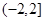 | C. | D. |
不等式(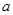 -2)
-2)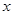 2+2(
2+2(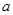 -2)
-2)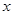 -4<0,对一切
-4<0,对一切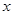 ∈R恒成立,则a的取值范围是( )
∈R恒成立,则a的取值范围是( )
| A.(-∞,2] | B.(-2,2] | C.(-2,2) | D.(-∞,2) |