题目内容
在R上定义运算 若不等式
若不等式 对任意实数
对任意实数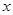 成立,则( )
成立,则( )
A. | B.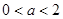 |
C.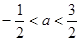 | D.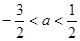 |
C
解析试题分析:∵(x-a)⊙(x+a)<1
∴(x-a)(1-x-a)<1,
即x2-x-a2+a+1>0
∵任意实数x成立,
故△=1-4(-a2+a+1)<0
∴- <a<
<a< ,
,
故选C.
考点:本题主要考查的是一道新定义的题,要遵守命题人定的规则,另外此题主要还是考查一元二次不等式的解法.
点评:解决该试题的关键是要将定义转化为关于x的一元二次不等式,然后结合二次不等式恒成立问题,得到判别式的范围,进而解得。

练习册系列答案
相关题目
关于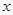 的不等式
的不等式 的解为
的解为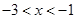 或
或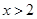 ,则
,则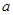 的取值为( )
的取值为( )
| A.2 | B.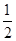 | C.-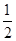 | D.-2 |
对一切实数x,不等式 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A. | B. | C. | D.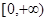 |
若不等式 成立的充分条件是
成立的充分条件是 ,则实数
,则实数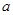 的取值范围是( )
的取值范围是( )
A.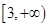 | B. | C. | D.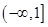 |
设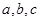 均为正数,且
均为正数,且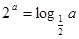 ,
,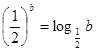 ,
,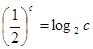 则( )
则( )
A. | B.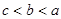 | C.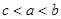 | D.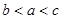 |
若不等式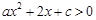 和
和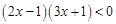 有相同的解集,则不等
有相同的解集,则不等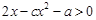 的解集是 ( )
的解集是 ( )
A. | B.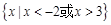 |
C.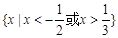 | D.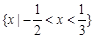 |
不等式 对于
对于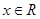 恒成立,那么
恒成立,那么 的取值范围是( )
的取值范围是( )
A. | B.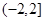 | C. | D. |
 的解集为( )
的解集为( )







 则关于
则关于 的不等式
的不等式 的解集是( )
的解集是( ) B
B
 D
D