题目内容
3.已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为${F_1},{F_2},{a^2}+{b^2}=4$,短轴端点B与两焦点F1,F2构成的三角形面积最大时,椭圆的短半轴长为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 a2+b2=4,即2b2+c2=4,利用基本不等式的性质可得bc≤$\sqrt{2}$,进而得出答案.
解答 解:∵a2+b2=4,∴2b2+c2=4≥2$\sqrt{2{b}^{2}•{c}^{2}}$,化为:bc≤$\sqrt{2}$,当且仅当c=$\sqrt{2}$b=$\sqrt{2}$时取等号.
∴${S}_{△{F}_{1}{F}_{2}B}$=$\frac{1}{2}×2c×b$=bc≤$\sqrt{2}$,此时取等号时,b=1,
故选:A.
点评 本题考查了椭圆的标准方程及其性质、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
13.复平面内若复数z=m2(1+i)-m(1+i)-6i所对应的点在第二象限,则实数m的取值范围是( )
| A. | (0,3) | B. | (-2,0) | C. | ∅ | D. | (-∞,-2) |
14.已知输入的x=11,执行如图所示的程序框图,则输出的x的值为( )


| A. | 23 | B. | 47 | C. | 95 | D. | 191 |
13.某大学生从全校学生中随机选取100名统计他们的鞋码大小,得到如下数据:
以各性别各鞋码出现的频率为概率.
(1)从该校随机挑选一名学生,求他(她)的鞋码为奇数的概率;
(2)为了解该校学生考试作弊的情况,从该校随机挑选120名学生进行抽样调查.每位学生从装有除颜色外无差别的4个红球和6个白球的口袋中,随机摸出两个球,若同色,则如实回答其鞋码是否为奇数;若不同色,则如实回答是否曾在考试中作弊.这里的回答,是指在纸上写下“是”或“否”.若调查人员回收到32张“是”的小纸条,试估计该校学生在考试中曾有作弊行为的概率.
| 鞋码 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 合计 |
| 男生 | - | - | 3 | 6 | 8 | 11 | 12 | 6 | 7 | 2 | 55 |
| 女生 | 4 | 6 | 12 | 9 | 9 | 2 | 2 | - | - | 1 | 45 |
(1)从该校随机挑选一名学生,求他(她)的鞋码为奇数的概率;
(2)为了解该校学生考试作弊的情况,从该校随机挑选120名学生进行抽样调查.每位学生从装有除颜色外无差别的4个红球和6个白球的口袋中,随机摸出两个球,若同色,则如实回答其鞋码是否为奇数;若不同色,则如实回答是否曾在考试中作弊.这里的回答,是指在纸上写下“是”或“否”.若调查人员回收到32张“是”的小纸条,试估计该校学生在考试中曾有作弊行为的概率.
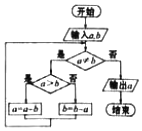 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为98,63,则输出的a为( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为98,63,则输出的a为( )