题目内容
12.已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=1-log2x,则不等式f(x)<0的解集是(-2,0)∪(2,+∞).分析 求出当x>0时,f(x)>0和f(x)<0的解集,利用奇函数的对称性得出当x<0时,f(x)<0的解集,从而得出f(x)<0的解集.
解答 解:当x>0,令f(x)<0,即1-log2x<0,解得x>2.
令f(x)>0即1-log2x>0,解得0<x<2.
∵f(x)是奇函数,
∴当x<0时,f(x)<0的解为-2<x<0.
故答案为:(-2,0)∪(2,+∞).
点评 本题考查了奇函数的性质,属于中档题.

练习册系列答案
相关题目
3.甲、乙、丙、丁四人站一排照相,其中甲、乙不相邻的站法共有n种,则($\root{3}{x}$-$\frac{1}{2x}$)n展开式的常数项为( )
| A. | -$\frac{55}{2}$ | B. | $\frac{55}{2}$ | C. | -55 | D. | 55 |
4.设复数z满足$\frac{1+z}{1-z}$=i,则z的虚部为( )
| A. | -i | B. | i | C. | 1 | D. | -1 |

 某几何体直观图与三视图如图所示,AB是⊙O的直径,PA垂直⊙O的直径,PA垂直⊙O所在的平面,C为圆周上一点.
某几何体直观图与三视图如图所示,AB是⊙O的直径,PA垂直⊙O的直径,PA垂直⊙O所在的平面,C为圆周上一点.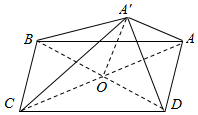 平行四边形ABCD中,AB=$\sqrt{13}$,BC=$\sqrt{5}$,BD=4,AC,BD交于O,将△ABD沿BD折起至△A′BD,使得A′C⊥CB.
平行四边形ABCD中,AB=$\sqrt{13}$,BC=$\sqrt{5}$,BD=4,AC,BD交于O,将△ABD沿BD折起至△A′BD,使得A′C⊥CB.