题目内容
1.设数列{an}满足a1+a2+…+an+2n=$\frac{1}{2}$(an+1+1),n∈N*,且a1=1,求证:(1)数列{an+2n}是等比数列;
(2)求数列{an}的前n项和Sn.
分析 (1)利用递推关系、等比数列的通项公式即可得出;
(2)利用等比数列的前n项和公式即可得出.
解答 (1)证明:∵a1+a2+…+an+2n=$\frac{1}{2}$(an+1+1),
∴当n≥2时,a1+a2+…+an-1+2n-1=$\frac{1}{2}$(an+1),
∴an+2n-1=$\frac{1}{2}({a}_{n+1}-{a}_{n})$,
化为an+1=3an+2n,
变形为:an+1+2n+1=3$({a}_{n}+{2}^{n})$,
∴数列{an+2n}是等比数列,首项为3,公比为3.
(2)解:由(1)可得:an+2n=3n,
∴an=3n-2n,
∴数列{an}的前n项和Sn=$\frac{3({3}^{n}-1)}{3-1}$-$\frac{2({2}^{n}-1)}{2-1}$=$\frac{{3}^{n+1}}{2}$-2n+1+$\frac{1}{2}$.
点评 本题考查了递推关系、等比数列的通项公式与前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.过点(2016,2016),且与直线2x-y-2015=0平行的直线是( )
| A. | 2x+y-2016=0 | B. | 2x-y-2016=0 | C. | 2x+y+2016=0 | D. | 2x-y+2016=0 |
11.设f′(x)是函数f(x)的导函数,且f′(x)>2f(x)(x∈R),f($\frac{1}{2}$)=e(e为自然对数的底数),则不等式f(lnx)<x2的解集为( )
| A. | (0,$\frac{e}{2}$) | B. | (0,$\sqrt{e}$) | C. | ($\frac{1}{e}$,$\frac{e}{2}$) | D. | ($\frac{e}{2}$,$\sqrt{e}$) |
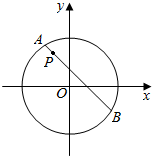 如图,圆O:x2+y2=8内有-点P(-1,2),AB为过P且倾斜角为135°的弦.
如图,圆O:x2+y2=8内有-点P(-1,2),AB为过P且倾斜角为135°的弦.