题目内容
19.函数f(x)=$\left\{\begin{array}{l}{1-{3}^{-x},x≥0}\\{{3}^{x}-1,x<0}\end{array}\right.$,则当x∈[1-a,+∞)时,不等式f(x-2a)+f(x)>0恒成立,则实数a的取值范围是(-∞,$\frac{1}{2}$).分析 分析函数的奇偶性和单调性,可将x∈[1-a,+∞)时,不等式f(x-2a)+f(x)>0恒成立,转化为x>a恒成立,将恒成立问题转化为最值问题,易得实数a的取值范围.
解答 解:函数f(x)=$\left\{\begin{array}{l}{1-{3}^{-x},x≥0}\\{{3}^{x}-1,x<0}\end{array}\right.$的图象如下图所示: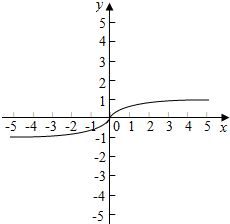
由图可得,函数在R上为增函数,且为奇函数,
∵当x∈[1-a,+∞)时,不等式f(x-2a)+f(x)>0恒成立,
∴当x∈[1-a,+∞)时,不等式f(x-2a)>-f(x)=f(-x)恒成立,
则1-a≤-x<x-2a,
即1-a>a,解得a<$\frac{1}{2}$,
∴实数a的取值范围是(-∞,$\frac{1}{2}$)
故答案为:(-∞,$\frac{1}{2}$)
点评 本题考查的知识点是奇偶性与单调性的综合,其中利用函数的性质,将已知中的不等式f(x-2a)+f(x)>0恒成立,转化为x>a恒成立,是解答的关键.

练习册系列答案
相关题目
7.平面上四点A,B,C,D,它们的坐标分别为A(-4,0),B(0,4),C(0,0),D(3cosα,3sinα),α∈(0,π).
(Ⅰ)若AB∥CD,求角α的值:
(Ⅱ)若AB⊥CD,求角α的值.
(Ⅰ)若AB∥CD,求角α的值:
(Ⅱ)若AB⊥CD,求角α的值.
11.设f′(x)是函数f(x)的导函数,且f′(x)>2f(x)(x∈R),f($\frac{1}{2}$)=e(e为自然对数的底数),则不等式f(lnx)<x2的解集为( )
| A. | (0,$\frac{e}{2}$) | B. | (0,$\sqrt{e}$) | C. | ($\frac{1}{e}$,$\frac{e}{2}$) | D. | ($\frac{e}{2}$,$\sqrt{e}$) |