题目内容
8.求下列三角函数值:(1)sin(-$\frac{π}{6}$);
(2)sin(-$\frac{7π}{4}$).
分析 利用三角函数诱导公式求解.
解答 解:(1)sin(-$\frac{π}{6}$)=-sin$\frac{π}{6}$=-$\frac{1}{2}$;
(2)sin(-$\frac{7π}{4}$)=-sin$\frac{7π}{4}$=-sin($2π-\frac{π}{4}$)=sin$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查三角函数值的求法,是基础题,解题时要认真审题,注意三角函数诱导公式的合理运用.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
18. 如图,在△ABC中,C=$\frac{π}{3}$,BC=4,点D在边AC上,AD=DB,DE⊥AB,E为垂足,若DE=2$\sqrt{2}$,则cosA等于( )
如图,在△ABC中,C=$\frac{π}{3}$,BC=4,点D在边AC上,AD=DB,DE⊥AB,E为垂足,若DE=2$\sqrt{2}$,则cosA等于( )
 如图,在△ABC中,C=$\frac{π}{3}$,BC=4,点D在边AC上,AD=DB,DE⊥AB,E为垂足,若DE=2$\sqrt{2}$,则cosA等于( )
如图,在△ABC中,C=$\frac{π}{3}$,BC=4,点D在边AC上,AD=DB,DE⊥AB,E为垂足,若DE=2$\sqrt{2}$,则cosA等于( )| A. | $\frac{2\sqrt{2}}{3}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{6}}{4}$ | D. | $\frac{\sqrt{6}}{3}$ |
17.圆(x+2)2+(y+2)2=4与圆(x-2)2+(y-1)2=9的公切线条数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.已知f′(x)是定义在R上的函数f(x)的导函数,且满足f′(x)>1,则不等式f(x)+2x+1>f(3x+1)的解集为( )
| A. | $\{x|x<-\frac{1}{2}\}$ | B. | {x|x<1} | C. | $\{x|x>-\frac{1}{2}\}$ | D. | {x|x>1} |
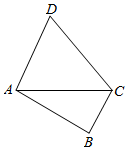 如图所示,在四边形ABCD中,已知AC=$\sqrt{6}+\sqrt{2}$,AD=2$\sqrt{2}$,DC=2$\sqrt{3}$,AD∥BC.
如图所示,在四边形ABCD中,已知AC=$\sqrt{6}+\sqrt{2}$,AD=2$\sqrt{2}$,DC=2$\sqrt{3}$,AD∥BC.