题目内容
323和391的最大公约数是（ ）
| A、21 | B、19 | C、17 | D、13 |
考点：用辗转相除计算最大公约数
专题：算法和程序框图
分析：根据辗转相除法计算即可：首先用大数除以小数，得到商和余数，然后再用上面的除数除以余数，又得到新的余数，如此继续做下去，直到刚好能够整除为止，得到两个数的最大公约数．
解答：
解：∵391÷323=1…68
323÷68=4…51
68÷51=1…17
51÷17=3
∴323和391的最大公约数是17．
故选：C．
323÷68=4…51
68÷51=1…17
51÷17=3
∴323和391的最大公约数是17．
故选：C．
点评：本题主要考查了“辗转相除法”，要熟练掌握其算法，属于基础题．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
下列各组函数中，表示同一函数的是（ ）
A、y=
| |||||
B、y=
| |||||
| C、y=lnex与y=elnx | |||||
D、y=x0与y=
|
三菱柱的侧棱与底面垂直，且底面是边长为2的等边三角形，其正视图（如图）的面积为8，则该三棱柱的体积为（ ）| A、4 | ||
B、4
| ||
C、8
| ||
| D、16 |
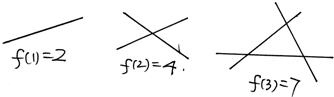对于问题：“两两相交且任三条不共点的n条直线把平面分为f（n）部分”，我们由归纳推理得到f（10）=（ ）| A、54 | B、55 | C、56 | D、57 |
下列说法正确的是（ ）
| A、函数的极大值就是函数的最大值 |
| B、函数的极小值就是函数的最小值 |
| C、函数的最值一定是极值 |
| D、在闭区间上的连续函数一定存在最值 |
已知双曲线
-
=1（a＞0，b＞0），右焦点F到渐近线的距离小于等于a，则该双曲线离心率的取值范围为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、（
| ||
B、[
| ||
C、（1，
| ||
D、（1，
|
在△ABC中，若a=7，b=8，cosC=
，则c=（ ）
| 13 |
| 14 |
| A、1 | B、2 | C、3 | D、4 |
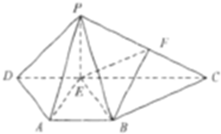如图，在四棱维P-ABCD中，侧面PCD⊥底面ABCD．四边形ABCD是等腰梯形．AB∥CD．∠ADC=∠PDC=