题目内容
已知函数y=f(x)是定义域为R的偶函数.当x≥0时,f(x)=
,若关于x的方程[f(x)]2+a•f(x)+b=0(a、b∈R)有且只有7个不同实数根,则a+b的值是 .
|
考点:分段函数的应用
专题:综合题,函数的性质及应用
分析:确定函数f(x)的性质,可得关于x的方程[f(x)]2+a•f(x)+b=0(a、b∈R)有且只有7个不同实数根,则方程t2+at+b=0必有两个根x1,x2,其中x1=1,x2∈(
,1),即可得出结论.
| 1 |
| 4 |
解答:
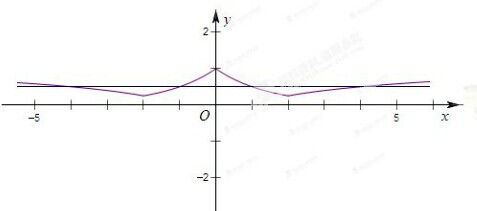 解:由题意,f(x)在(-∞,-2]和[0,2]上是减函数,在[-2,0]和[2,+∞)上是增函数,
解:由题意,f(x)在(-∞,-2]和[0,2]上是减函数,在[-2,0]和[2,+∞)上是增函数,
∴x=0时,函数取极大值1,x=±2时,取极小值
,|x|≥16时,f(x)≥1,
∴关于x的方程[f(x)]2+a•f(x)+b=0(a、b∈R)有且只有7个不同实数根,
则方程t2+at+b=0必有两个根x1,x2,其中x1=1,x2∈(
,1),
∴1+a+b=0,
∴a+b=-1.
故答案为:-1.
 解:由题意,f(x)在(-∞,-2]和[0,2]上是减函数,在[-2,0]和[2,+∞)上是增函数,
解:由题意,f(x)在(-∞,-2]和[0,2]上是减函数,在[-2,0]和[2,+∞)上是增函数,∴x=0时,函数取极大值1,x=±2时,取极小值
| 1 |
| 4 |
∴关于x的方程[f(x)]2+a•f(x)+b=0(a、b∈R)有且只有7个不同实数根,
则方程t2+at+b=0必有两个根x1,x2,其中x1=1,x2∈(
| 1 |
| 4 |
∴1+a+b=0,
∴a+b=-1.
故答案为:-1.
点评:本题考查分段函数的应用,考查函数的性质,考查数形结合的数学思想,正确确定函数的性质是关键.

练习册系列答案
相关题目
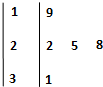 已知某篮球运动员2013年度参加了25场比赛,若从中抽取5场,用茎叶图统计该运动员5场中的得分如图所示,则该样本的方差为 ( )
已知某篮球运动员2013年度参加了25场比赛,若从中抽取5场,用茎叶图统计该运动员5场中的得分如图所示,则该样本的方差为 ( )| A、4 | ||
B、
| ||
| C、18 | ||
| D、16 |
如果一扇形的弧长为π,半径等于2,则扇形所对圆心角为( )
| A、π | ||
| B、2π | ||
C、
| ||
D、
|
