题目内容
下列方程所表示的曲线中，关于x轴和y轴都对称的是（ ）
| A、x2-y2=1 |
| B、y2=x |
| C、（x-1）2+y2=1 |
| D、x-y+1=0 |
考点：曲线与方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据关于x轴对称，（x，y）与（x，-y）都在曲线上，关于y轴都对称，（x，y）与（-x，y）都在曲线上，即可得出结论．
解答：
解：根据关于x轴对称，（x，y）与（x，-y）都在曲线上，关于y轴都对称，（x，y）与（-x，y）都在曲线上，
可得x2-y2=1满足题意，
故选：A．
可得x2-y2=1满足题意，
故选：A．
点评：本题考查轨迹方程，考查曲线的对称性，考查学生分析解决问题的能力，属于基础题．
练习册系列答案
相关题目
不等式
≤0的解集为（ ）
| x |
| x+1 |
| A、[-1，0] | B、[-1，0） |
| C、（-1，0] | D、R |
已知cosα=
，cosβ=
，且α，β∈（0，
），则cos（α-β）=（ ）
| 1 |
| 3 |
| 7 |
| 9 |
| π |
| 2 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
给出下列等式
①
=
②
=a
③{y|y=-x2+x-1，x≥1}∩{x|x=
-2，m≥0}={-1}
④{x||1-2x|＜5}∪{x|6-x-x2＞0}={x|-
＞0}
则上述等式成立的是（ ）
①
log51-log5
|
| 1-2log52 |
②
| a6 | ||||
|
| 6 |
| 5 |
③{y|y=-x2+x-1，x≥1}∩{x|x=
| m+1 |
④{x||1-2x|＜5}∪{x|6-x-x2＞0}={x|-
| x+3 |
| x-3 |
则上述等式成立的是（ ）
| A、①③ | B、①② | C、①④ | D、①③④ |
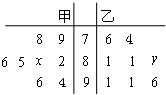某中学高三年级从甲、乙两个班级各选出8名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生成绩的平均分是86，乙班学生成绩的中位数是83，则x+y的值为（ ）| A、9 | B、10 | C、11 | D、13 |
若1和a的等差中项是2，则a的值为（ ）
| A、4 | B、3 | C、1 | D、-4 |