题目内容
解方程:
(1)3x-5x-2=3x-4-5x-3;
(2)logx(9x2)•log32x=4.
(1)3x-5x-2=3x-4-5x-3;
(2)logx(9x2)•log32x=4.
考点:对数的运算性质,有理数指数幂的运算性质
专题:函数的性质及应用
分析:(1)根据指数方程的解法,解方程即可.
(2)根据对数的运算法则,解对数方程即可得到结论.
(2)根据对数的运算法则,解对数方程即可得到结论.
解答:
解:(1)由3x-5x-2=3x-4-5x-3,得3x-3x-4=5x-2-5x-3;
即3x-4(34-1)=5x-3(5-1),
即80×3x-4=4×5x-3;
即20×3x-4=5×5x-4;
∴4×3x-4=5x-4,
即4=(
)x-4;
解得:x-4=log
4,
∴x=4+log
4;
故方程的解为x=4+log
4;
(2)∵logx(9x2)•log32x=4.
∴[logx9+logxx2]log32x=4.
即[2logx3+2]•log32x=4.
∴2log3x+2log32x=4,
∴log32x+log3x-2=0,
解得log3x=1,或log3x=-2,
即x=3或x=
.
当x=3时,logx(9x2)•log32x=log3(9×32)•log323=4成立,
当x=
时,logx(9x2)•log32x=log
(9×(
)2)•log32
=4成立.
故方程的解是x=3或x=
.
即3x-4(34-1)=5x-3(5-1),
即80×3x-4=4×5x-3;
即20×3x-4=5×5x-4;
∴4×3x-4=5x-4,
即4=(
| 5 |
| 3 |
解得:x-4=log
| 5 |
| 3 |
∴x=4+log
| 5 |
| 3 |
故方程的解为x=4+log
| 5 |
| 3 |
(2)∵logx(9x2)•log32x=4.
∴[logx9+logxx2]log32x=4.
即[2logx3+2]•log32x=4.
∴2log3x+2log32x=4,
∴log32x+log3x-2=0,
解得log3x=1,或log3x=-2,
即x=3或x=
| 1 |
| 9 |
当x=3时,logx(9x2)•log32x=log3(9×32)•log323=4成立,
当x=
| 1 |
| 9 |
| 1 |
| 9 |
| 1 |
| 9 |
| 1 |
| 9 |
故方程的解是x=3或x=
| 1 |
| 9 |
点评:本题主要考查指数方程和对数方程的求解,根据指数幂和对数的运算法则是解决本题的关键,考查学生的计算能力.

练习册系列答案
相关题目
下列方程所表示的曲线中,关于x轴和y轴都对称的是( )
| A、x2-y2=1 |
| B、y2=x |
| C、(x-1)2+y2=1 |
| D、x-y+1=0 |
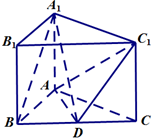 如图三棱柱ABC-A1B1C1中,侧棱与底面垂直,△ABC是等边三角形,点D是BC的中点.
如图三棱柱ABC-A1B1C1中,侧棱与底面垂直,△ABC是等边三角形,点D是BC的中点.
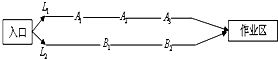 某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入之后有L1,L2两条巷道通往作业区(如图),L1巷道有A1,A2,A3三个易堵塞点,各点被堵塞的概率都是
某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入之后有L1,L2两条巷道通往作业区(如图),L1巷道有A1,A2,A3三个易堵塞点,各点被堵塞的概率都是