题目内容
已知函数f(x)=sinx-sin(x-
)
(Ⅰ)求f(
);
(Ⅱ)求f(x)在[-
,
]上的取值范围.
| π |
| 3 |
(Ⅰ)求f(
| π |
| 6 |
(Ⅱ)求f(x)在[-
| π |
| 2 |
| π |
| 2 |
考点:两角和与差的正弦函数,三角函数中的恒等变换应用
专题:三角函数的求值
分析:(Ⅰ)根据函数f(x)的解析式,直接求得 f(
)=sin
-sin(
-
) 的值.
(Ⅱ)化简函数的解析式为f(x)=sin(x+
),根据-
≤x≤
,利用正弦函数的定义域和值域求得f(x)的取值范围.
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
(Ⅱ)化简函数的解析式为f(x)=sin(x+
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
解答:
解:(Ⅰ)由题意可得 f(
)=sin
-sin(
-
)=sin
-sin(-
)=sin
+sin
=2sin
=1.
(Ⅱ)∵f(x)=sinx-
sinx+
cosx=
sinx+
cosx=sin(x+
),
∵-
≤x≤
,∴-
≤x+
≤
,-
≤sin(x+
)≤1,
所以,f(x)的取值范围是[-
,1].
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
(Ⅱ)∵f(x)=sinx-
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
∵-
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
所以,f(x)的取值范围是[-
| 1 |
| 2 |
点评:本题主要考查三角函数的恒等变换,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案
相关题目
在复平面内,复数
的共轭复数对应的点在第( )象限.
| i |
| 1+i |
| A、一 | B、二 | C、三 | D、四 |
下列方程所表示的曲线中,关于x轴和y轴都对称的是( )
| A、x2-y2=1 |
| B、y2=x |
| C、(x-1)2+y2=1 |
| D、x-y+1=0 |
由a1=1,an+1=
给出的数列{an}的第33项是( )
| an |
| 3an+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
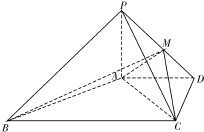 如图四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,ADCD,且AD=CD=2
如图四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,ADCD,且AD=CD=2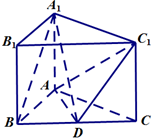 如图三棱柱ABC-A1B1C1中,侧棱与底面垂直,△ABC是等边三角形,点D是BC的中点.
如图三棱柱ABC-A1B1C1中,侧棱与底面垂直,△ABC是等边三角形,点D是BC的中点.