题目内容
2.己知关于x的方程x2-px+1=0的两个根是x1,x2,且|x1-x2|=3,求实数p的值.分析 根据一元二次方程根与系数的关系,结合题意列出方程,解方程即可求出p的值.
解答 解:∵x1,x2是方程x2-px+1=0的两个根,
∴x1+x2=p,x1•x2=1,
又|x1-x2|=3,
∴${{(x}_{1}{+x}_{2})}^{2}$-4x1x2=9,
即p2-4×1=9,
解得p=±$\sqrt{13}$.
点评 本题考查了一元二次方程的根与系数关系的应用问题,是基础题目.

练习册系列答案
相关题目
12.已知集合A={x|(x+1)(x-2)≤0},B={x|x-1>0},则A∩B=( )
| A. | [-2,1) | B. | (1,+∞) | C. | (1,2] | D. | (2,+∞) |
7.下列各组中的两个函数是同一函数的是( )
| A. | f(x)=lgx+lg(x-1),g(x)=lg[x(x-1)] | B. | f(x)=$\frac{\sqrt{1-{x}^{2}}}{|x+2|-2}$,g(x)=$\frac{\sqrt{1-{x}^{2}}}{x}$ | ||
| C. | y=f(x)与y=f(x-3) | D. | f(x)=|x|+|x-1|,g(x)=2x-1 |
14.已知函数f(x)是偶函数,且当x≥0时,f(x)=log2(x+1)-x2,则f(f(3))=( )
| A. | -7 | B. | -46 | C. | 7 | D. | 46 |
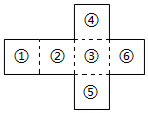 如图是一个正方体纸盒的展开图,把复数1,-1,2i,-2i,$\sqrt{2}$,-$\sqrt{2}$按虚线分别填入六个正方折成正方体后,相对面上的两个数的模相等,则不同的填法有48种(用数字作答)
如图是一个正方体纸盒的展开图,把复数1,-1,2i,-2i,$\sqrt{2}$,-$\sqrt{2}$按虚线分别填入六个正方折成正方体后,相对面上的两个数的模相等,则不同的填法有48种(用数字作答)