题目内容
11.已知数列{an}的各项均为正数,且满足2an+1+$\frac{1}{{a}_{n+1}}$=an$+\frac{2}{{a}_{n}}$(n∈N*),且使得a1=a2016成立的a1的值是1.分析 满足2an+1+$\frac{1}{{a}_{n+1}}$=an$+\frac{2}{{a}_{n}}$(n∈N*),化为:(2an+1-an)$(1-\frac{1}{{a}_{n}{a}_{n+1}})$=0,可得${a}_{n+1}=\frac{1}{2}{a}_{n}$,或anan+1=1,由${a}_{n+1}=\frac{1}{2}{a}_{n}$,可得数列{an}为单调数列,不可能有a1=a2016成立,舍去.由anan+1=1,可得an=an+2.使得a1=a2016成立,可得a1=a2,即可得出.
解答 解:∵满足2an+1+$\frac{1}{{a}_{n+1}}$=an$+\frac{2}{{a}_{n}}$(n∈N*),
化为:(2an+1-an)$(1-\frac{1}{{a}_{n}{a}_{n+1}})$=0,
可得${a}_{n+1}=\frac{1}{2}{a}_{n}$,或anan+1=1,
由${a}_{n+1}=\frac{1}{2}{a}_{n}$,可得数列{an}为单调数列,不可能有a1=a2016成立.
由anan+1=1,可得an+1an+2=1,
∴an=an+2.
∴a1=a3=…,
a2=a4=…=a2016.
使得a1=a2016成立,又a1,a2>0,a1a2=1,
∴a1=a2,
解得a1=1.
使得a1=a2016成立的a1的值是1.
故答案为:1.
点评 本题考查了递推关系、数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.已知集合A={x|x=sin$\frac{nπ}{6}$,n∈z},则该集合中所有元素之和为( )
| A. | -3-$\sqrt{3}$ | B. | 0 | C. | $\frac{3+\sqrt{3}}{2}$ | D. | 3+$\sqrt{3}$ |
20.命题p:x>y是命题q:x-3>y-4的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.将函数f(x)=sin(2x+ϕ),$(|ϕ|<\frac{π}{2})$的图象沿x轴向左平移$\frac{π}{8}$个单位后,得到一个偶函数g(x)的图象,则函数g(x)的一个减区间为( )
| A. | $[{-\frac{π}{4},\frac{π}{4}}]$ | B. | $[{-\frac{π}{2},0}]$ | C. | $[{0,\frac{π}{2}}]$ | D. | $[{\frac{π}{4},\frac{3π}{4}}]$ |
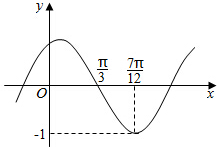 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示.