题目内容
如图10-8,在三棱锥S—ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2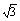 ,M、N分别为AB、SB的中点。
,M、N分别为AB、SB的中点。
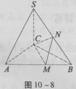 (1)证明:AC⊥SB;
(1)证明:AC⊥SB;
(2)求二面角N—CM—B的大小;
(3)求点B到平面CMN的距离。
 (3)在Rt△NEF中,NF=
(3)在Rt△NEF中,NF=
∴S△CMN= CM·NF=
CM·NF= ,S△CMB=
,S△CMB= BM·CM=2
BM·CM=2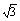 .设点B到平面CMN的距离为h, ∵VB—CMN=VN-CMB,NE⊥平面CMB,∴
.设点B到平面CMN的距离为h, ∵VB—CMN=VN-CMB,NE⊥平面CMB,∴ S△CMN·h=
S△CMN·h= S△CMB·NE,∴h=
S△CMB·NE,∴h= 即点B到
即点B到 平面CMN的距离为
平面CMN的距离为 。
。

练习册系列答案
相关题目
 1.计算a2、a3、a4,然后猜想an的表达式。并证明你的结论。
1.计算a2、a3、a4,然后猜想an的表达式。并证明你的结论。 与圆
与圆
 ( )
( )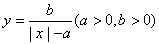 与
与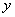 轴的交点关于原点的对称点称为“望点”,以“望点”为圆心,凡是与曲线C有公共点的圆,皆称之为“望圆”,则当a=1,b=1时,所有的“望圆”中,面积最小的“望圆”的面积为 .
轴的交点关于原点的对称点称为“望点”,以“望点”为圆心,凡是与曲线C有公共点的圆,皆称之为“望圆”,则当a=1,b=1时,所有的“望圆”中,面积最小的“望圆”的面积为 . 为圆
为圆 外一点,由
外一点,由 与圆
与圆 点,引圆
点,引圆 与圆
与圆 点.已知
点.已知 ,
,  .则圆
.则圆
 平面
平面 ,
, 过平面
过平面 与
与 都成
都成 角的直线有且只有:( )
角的直线有且只有:( )
 的整数m,n作为点P(m,n)的坐标,则点P落在圆x2+y2=16内的概率为________.
的整数m,n作为点P(m,n)的坐标,则点P落在圆x2+y2=16内的概率为________.