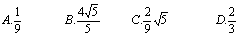题目内容
如图10-4所示，在正三棱锥A—BCD中，∠BAC=30°，AB=a，平行于AD、BC的截面EFGH分别交AB、BD、DC、CA于E、F、G、H。
（1）判定四边形EFGH的形状，并说明理由；
（2）设P是棱AD上的点，当AP为何值时，平面PBC⊥平面EFGH，请给出证明。
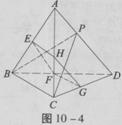
（2）作CP⊥AD于P点，连接BP，∵AD⊥BC，∴AD⊥面BCP，∴HG∥AD，∴HG⊥面BCP，又HG
面EFGH，∴面BCP⊥面EFGH，在Rt△APC中，∠CAP=30°，AC=a, ∴AP=
.
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
则
（ ）
D．
作圆
的弦
，使得点
平分弦
，M、N分别为AB、SB的中点。
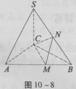（1）证明：AC⊥SB；
= l，点A∈α，A
l，直线AB∥l，直线AC⊥l，直线m∥α
C的取值范围。
