题目内容
对任意实数a,b,定义F(a,b)=
(a+b-|a-b|),如果函数f(x)=ln(e2x),g(x)=3-x,那么G(x)=F(f(x),g(x))的最大值为 .
| 1 |
| 2 |
考点:函数的最值及其几何意义
专题:数形结合
分析:“对任意实数a,b,定义:定义F(a,b)=
(a+b-|a-b|)”的意思是两个函数的函数值进行比较,较大的舍去留下较小的函数值,结合图象即可求出函数值.
| 1 |
| 2 |
解答:
解::“对任意实数a,b,定义:定义F(a,b)=
(a+b-|a-b|)”的意思是两个函数的函数值进行比较,
较大的舍去留下较小的函数值.
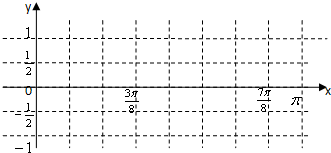
∵f(x)=ln(e2x)=2+lnx,g(x)=3-x,
如图示:
故G(x)的最大值等于2.
故答案为:2.
| 1 |
| 2 |
较大的舍去留下较小的函数值.
∵f(x)=ln(e2x)=2+lnx,g(x)=3-x,
如图示:

故G(x)的最大值等于2.
故答案为:2.
点评:本题主要考查了函数的最值及其几何意义,以及数形结合的数学思想,属于基础题.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目