题目内容
13.设函数f(x)=ex-ax,a是常数.(Ⅰ)若a=1,且曲线y=f(x)的切线l经过坐标原点(0,0),求该切线的方程;
(Ⅱ)讨论f(x)的零点的个数.
分析 (Ⅰ)求出函数的导数,表示出切线方程,求出m的值,从而求出切线方程即可;
(Ⅱ)求出函数f(x)的导数,通过讨论 a的范围,求出函数的单调区间,从而求出函数的零点个数即可.
解答 解:(Ⅰ)a=1时,f(x)=ex-x,f′(x)=ex-1 …(1分),
设切点坐标是(m,em-m),
则k=f′(m)=em-1,
故切线方程是:
y-(em-m)=(em-1)(x-m) …(3分)
由0-(em-m)=(em-1)(0-m),得m=1,
所求切线为:y=(e-1)x…(5分)
(Ⅱ)f′(x)=ex-a,当a>0时,由f′(x)=0得x=lna…(6分)
(1)a>0时,若x<lna,则f′(x)<0;若x>lna,则f′(x)>0.
函数f(x)在区间(-∞,lna)单调递减,在区间(lna,+∞)单调递增,
f(x)的最小值为f(lna)=a(1-lna)…(7分)
①0<a<e时,f(lna)=a(1-lna)>0,f(x)无零点…(8分)
②a=e时,f(lna)=a(1-lna)=0,f(x)只有一个零点…(9分)
③a>e时,f(lna)=a(1-lna)<0,根据f(0)=1>0与函数的单调性,
f(x)在区间(-∞,lna)和(lna,+∞)各有一个零点,f(x)共有两个零点…(10分)
(2)a=0时,f(x)=ex,f(x)无零点…(11分)
(3)a<0时,由f(x)=0得,ex=ax,
故曲线y=ex与y=ax只有一个交点,所以f(x)只有一个零点.
综上所述,0≤a<e时,f(x)无零点;
a<0或a=e时,f(x)有一个零点;
a>e时,f(x)有两个零点…(12分)
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道综合题.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案 如图,在三棱锥A-BCD中,平面ABC⊥平面BCD,△BAC与△BCD均为等腰直角三角形,且∠BAC=∠BCD=90°,BC=2,点P是线段AB上的动点,若线段CD上存在点Q,使得异面直线PQ与AC成30°的角,则线段PA长的取值范围是( )
如图,在三棱锥A-BCD中,平面ABC⊥平面BCD,△BAC与△BCD均为等腰直角三角形,且∠BAC=∠BCD=90°,BC=2,点P是线段AB上的动点,若线段CD上存在点Q,使得异面直线PQ与AC成30°的角,则线段PA长的取值范围是( )| A. | (0,$\frac{\sqrt{2}}{2}$) | B. | (0,$\frac{\sqrt{6}}{3}$) | C. | ($\frac{\sqrt{2}}{2}$,$\sqrt{2}$) | D. | ($\frac{\sqrt{6}}{3}$,$\sqrt{2}$) |
 下面的茎叶图表示连续多天同一路口同一时段通过车辆的数目,则这些车辆数的中位数和众数分别是( )
下面的茎叶图表示连续多天同一路口同一时段通过车辆的数目,则这些车辆数的中位数和众数分别是( )| A. | 230.5,220 | B. | 231.5,232 | C. | 231,231 | D. | 232,231 |

| A. | 335 | B. | 336 | C. | 337 | D. | 338 |
| A. | $\frac{3-2\sqrt{2}}{8}$ | B. | $\frac{2-\sqrt{2}}{4}$ | C. | $\frac{5-2\sqrt{2}}{8}$ | D. | $\frac{5-2\sqrt{2}}{4}$ |
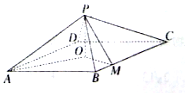 如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面$ABCD,AB=2,∠BAD=\frac{π}{3},M$为BC上一点,且$BM=\frac{1}{2}$.
如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面$ABCD,AB=2,∠BAD=\frac{π}{3},M$为BC上一点,且$BM=\frac{1}{2}$. 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为等腰梯形,AB∥CD,AD=DC=BC=2,AB=4,△PAD为正三角形.
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为等腰梯形,AB∥CD,AD=DC=BC=2,AB=4,△PAD为正三角形.