题目内容
3. 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为等腰梯形,AB∥CD,AD=DC=BC=2,AB=4,△PAD为正三角形.
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为等腰梯形,AB∥CD,AD=DC=BC=2,AB=4,△PAD为正三角形.(Ⅰ)求证:BD⊥平面PAD;
(Ⅱ)设AD的中点为E,求平面PEB与平面PDC所成二面角的平面角的余弦值.
分析 (Ⅰ)在等腰梯形ABCD中,过点D作DE⊥AB于点E,推导出AD⊥BD,由此能证明BD⊥平面PAD.
(Ⅱ)以D为坐标原点,DA所在直线为x轴,DB所在直线为y轴,过点D平行于PE所在直线为z轴,建立空间直角坐标系.利用向量法能求出平面PEB与平面PDC所成二面角的余弦值.
解答 证明:(Ⅰ)在等腰梯形ABCD中,过点D作DE⊥AB于点E,
如图所示:有$AE=1,DE=\sqrt{3},BD=2\sqrt{3}$
∴在△ABD中,有AB2=AD2+BD2,即AD⊥BD
又因为平面PAD⊥平面ABCD且交线为AD,∴BD⊥平面PAD.-----(5分)
解:(Ⅱ) 由平面PAD⊥平面ABCD,且△PAD为正三角形,E为AD的中点,
∴PE⊥AD,得PE⊥平面ABCD.
如图所示,以D为坐标原点,DA所在直线为x轴,DB所在直线为y轴,过点D平行于PE所在直线为z轴,建立空间直角坐标系.
由条件AD=DC=BC=2,则AE=DE=1,$PE=\sqrt{3}$,$BD=2\sqrt{3}$.
则D(0,0,0),E(1,0,0),$B(0,2\sqrt{3},0)$,$P(1,0,\sqrt{3})$.-------(6分)
在等腰梯形ABCD中,过点C作BD的平行线交AD延长线于点F如图所示:
则在Rt△CDF中,有$CF=\sqrt{3}$,DF=1,∴$C(-1,\sqrt{3},0)$.-------(7分)
(另解:可不作辅助线,利用$\overrightarrow{AB}=2\overrightarrow{DC}$求点C坐标)
∴$\overrightarrow{CD}=(1,-\sqrt{3},0)$,$\overrightarrow{PD}=(-1,0,-\sqrt{3})$,设平面PDC的法向量$\overrightarrow{n_1}=({x_1},{y_1},{z_1})$
则$\left\{{\begin{array}{l}{\overrightarrow{n_1}•\overrightarrow{CD}={x_1}-\sqrt{3}{y_1}=0\;}\\{\overrightarrow{n_1}•\overrightarrow{PD}=-{x_1}-\sqrt{3}{z_1}=0}\end{array}}\right.$,取${x_1}=\sqrt{3}$,则y1=1,z1=-1,
∴面PDC的法向量$\overrightarrow{n_1}=(\sqrt{3},1,-1)$.-------(9分)
同理有$\overrightarrow{PE}=(0,0,-\sqrt{3})$,$\overrightarrow{PB}=(-1,2\sqrt{3},-\sqrt{3})$,设平面PBE的法向量$\overrightarrow{n_2}=({x_2},{y_2},{z_2})$
则$\left\{{\begin{array}{l}{\overrightarrow{n_2}•\overrightarrow{PE}=-\sqrt{3}{z_2}=0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\\{\overrightarrow{n_2}•\overrightarrow{PB}=-{x_2}+2\sqrt{3}{y_2}-\sqrt{3}{z_2}=0}\end{array}}\right.$,
取y2=1,则${x_2}=2\sqrt{3}$,z2=0,∴面PBE的法向量$\overrightarrow{n_2}=(2\sqrt{3},1,0)$.--(10分)
设平面PEB与平面PDC所成二面角的平面角为θ,
∴$cosθ=|{cos<\overrightarrow{n_1},\overrightarrow{n_2}>}|=|{\frac{{\sqrt{3}×2\sqrt{3}+1}}{{\sqrt{3+1+1}×\sqrt{12+1}}}}|=\frac{{7\sqrt{65}}}{65}$.
即平面PEB与平面PDC所成二面角的余弦值为$\frac{{7\sqrt{65}}}{65}$.-------(12分)
点评 本题考查线面垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

| A. | {a1|a1≥2017,a1∈N+} | B. | {a1|a1≥2016,a1∈N+} | C. | {a1|a1≥2015,a1∈N+} | D. | {a1|a1≥2014,a1∈N+} |
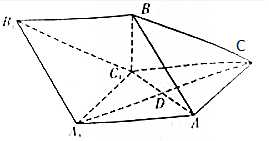 如图,三棱柱ABC-A1B1C1中,AC=AA1=2,AB=BC=2$\sqrt{2}$,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.
如图,三棱柱ABC-A1B1C1中,AC=AA1=2,AB=BC=2$\sqrt{2}$,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D. 如图所示,在三棱锥P-ABC中,已知PC⊥平面ABC,点C在平面PBA内的射影D在直线PB上.
如图所示,在三棱锥P-ABC中,已知PC⊥平面ABC,点C在平面PBA内的射影D在直线PB上.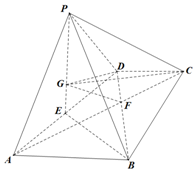 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为梯形,AB∥CD,AB=2DC=2$\sqrt{3}$,AC∩BD=F.且△PAD与△ABD均为正三角形,E为AD的中点,G为△PAD重心.
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为梯形,AB∥CD,AB=2DC=2$\sqrt{3}$,AC∩BD=F.且△PAD与△ABD均为正三角形,E为AD的中点,G为△PAD重心. 已知如图:三棱柱ABC-A1B1C1的各条棱均相等,AA1⊥平面ABC,E为AA1的中点.
已知如图:三棱柱ABC-A1B1C1的各条棱均相等,AA1⊥平面ABC,E为AA1的中点.