题目内容
5.点M(3,2)到拋物线C:y=ax2(a>0)准线的距离为4,F为拋物线的焦点,点N(l,l),当点P在直线l:x-y=2上运动时,$\frac{|PN|-1}{|PF|}$的最小值为( )| A. | $\frac{3-2\sqrt{2}}{8}$ | B. | $\frac{2-\sqrt{2}}{4}$ | C. | $\frac{5-2\sqrt{2}}{8}$ | D. | $\frac{5-2\sqrt{2}}{4}$ |
分析 先求出抛物线的方程,设AP=t,则AN=$\sqrt{2}$,AF=2$\sqrt{2}$,PN=$\sqrt{{t}^{2}+2}$,PF=$\sqrt{{t}^{2}+8}$,再表示$\frac{|PN|-1}{|PF|}$,利用换元法,即可得出结论.
解答 解:∵点M(3,2)到拋物线C:y=ax2(a>0)准线的距离为4,
∴2+$\frac{1}{4a}$=4,∴a=$\frac{1}{8}$,∴拋物线C:x2=8y,
直线l:x-y=2与x轴交于A(2,0),则FA⊥l.
设AP=t,则AN=$\sqrt{2}$,AF=2$\sqrt{2}$,PN=$\sqrt{{t}^{2}+2}$,PF=$\sqrt{{t}^{2}+8}$,
设$\sqrt{{t}^{2}+2}$-1=m(m≥$\sqrt{2}$-1),则$\frac{|PN|-1}{|PF|}$=$\frac{\sqrt{{t}^{2}+2}-1}{\sqrt{{t}^{2}+8}}$=$\frac{m}{\sqrt{(m+1)^{2}+6}}$=$\frac{1}{\sqrt{7(\frac{1}{m}+\frac{1}{7})^{2}+\frac{6}{7}}}$,
∴m=$\sqrt{2}$-1,即t=0时,$\frac{|PN|-1}{|PF|}$的最小值为$\frac{2-\sqrt{2}}{4}$.
故选:B.
点评 本题考查抛物线的方程与性质,考查$\frac{|PN|-1}{|PF|}$的最小值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 如图是甲、乙汽车4S店7个月销售汽车数量(单位:台)的茎叶图,若x是4与6的等差中项,y是2和8的等比中项,设甲店销售汽车的众数是a,乙店销售汽车中位数为b,则a+b的值为( )
如图是甲、乙汽车4S店7个月销售汽车数量(单位:台)的茎叶图,若x是4与6的等差中项,y是2和8的等比中项,设甲店销售汽车的众数是a,乙店销售汽车中位数为b,则a+b的值为( )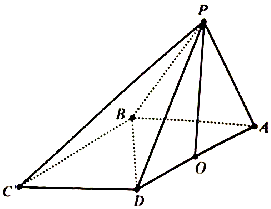 在四棱锥P-ABCD中,$∠DBA=\frac{π}{2}$,$AB\underline{\underline∥}CD$,△PAB和△PBD都是边长为2的等边三角形,设P在底面ABCD的射影为O.
在四棱锥P-ABCD中,$∠DBA=\frac{π}{2}$,$AB\underline{\underline∥}CD$,△PAB和△PBD都是边长为2的等边三角形,设P在底面ABCD的射影为O.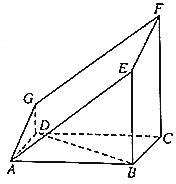 如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.
如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.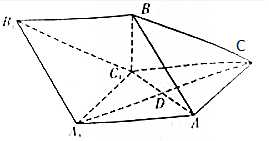 如图,三棱柱ABC-A1B1C1中,AC=AA1=2,AB=BC=2$\sqrt{2}$,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.
如图,三棱柱ABC-A1B1C1中,AC=AA1=2,AB=BC=2$\sqrt{2}$,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D. 已知如图:三棱柱ABC-A1B1C1的各条棱均相等,AA1⊥平面ABC,E为AA1的中点.
已知如图:三棱柱ABC-A1B1C1的各条棱均相等,AA1⊥平面ABC,E为AA1的中点.