题目内容

若1＜x＜10，那么（lgx）2，lgx2，lg（lgx）的大小顺序是（　　）
A、（lgx）2＜lg（lgx）＜lgx2
B、（lgx）2＜lgx2＜lg（lgx）
C、lgx2＜（lgx）2＜lg（lgx）
D、lg（lgx）＜（lgx）2＜lgx2
考点：对数值大小的比较
专题：函数的性质及应用
分析：1＜x＜10，可得0＜lgx＜1．于是lg（lgx）＜0，（lgx）2-lgx2=lgx（lgx-2）＜0，即可得出．
解答： 解：∵1＜x＜10，
∴0＜lgx＜1．
∴lg（lgx）＜0，（lgx）2-lgx2=lgx（lgx-2）＜0，即0＜（lgx）2＜lgx2，
∴lg（lgx）＜（lgx）2＜lgx2，
故选：D．
点评：本题考查了对数的运算法则及其对数函数的单调性，考查了计算能力，属于基础题．
练习册系列答案
相关题目
下列五个命题中：
①函数y=loga（2x-1）+2015（a＞0且a≠1）的图象过定点（1，2015）；
②若定义域为R函数f（x）满足：对任意互不相等的x1、x2都有（x1-x2）[f（x1）-f（x2）]＞0，则f（x）是减函数；
③f（x+1）=x2-1，则f（x）=x2-2x；
④若函数f（x）=
a•2x+a-2
2x+1
是奇函数，则实数a=-1；
⑤若a=
logc8
logc2
（c＞0，c≠1），则实数a=3．
其中正确的命题是
 
．（填上相应的序号）．
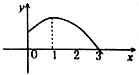
函数y=sin（ωx+φ）的部分图象如图，则φ、ω可以取的一组值是（　　）
A、ω=
π
2
，φ=
π
4
B、ω=
π
4
，φ=
π
4
C、ω=
π
3
，φ=
π
6
D、ω=
π
4
，φ=
5π
4
若loga
3
4
≥1，则a的取值范围是
 
．
已知函数f（x）满足3f（x）-f（
1
x
）=2x，则f（x）=（　　）
A、
1
4x
+
3x
4
B、
1
4x
-
3x
4
C、-
1
4x
-
3x
4
D、-
1
4x
+
3x
4
已知集合A={x2-3x-10≤0}，B={x|m-1＜x＜2m+1}
（Ⅰ）当m=3时，求A∩B．
（Ⅱ）若B⊆A，求实数m的取值范围．
函数y=f（x），x∈[a，b]的图象与x=1的交点个数是（　　）
A、1B、2C、0或1D、1或2
已知直线l：x-2y-1=0，直线l1过点（-1，2）．
（1）若l1⊥l，求直线l1与l的交点坐标；
（2）若l1∥l，求直线l1的方程．
下列函数f（x）与g（x）相等的一组是（　　）
A、f（x）=x-1，g（x）=
x2
x
-1
B、f（x）=x2，g（x）=（
x
）4
C、f（x）=log2x2，g（x）=2log2x
D、f（x）=tanx，g（x）=
sinx
cosx

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网