题目内容
下列命题中正确命题的个数是( )
①“数列{an}既是等差数列,又是等比数列”的充要条件是“数列{an}是常数列”;
②不等式|x-1|+|y-1|≤1表示的平面区域是一个菱形及其内部;
③f(x)是(-∞,0)∪(0,+∞)上的奇函数,x>0时的解析式是f(x)=2x,则x<0时的解析式为f(x)=-2-x;
④若两个非零向量
、
共线,则存在两个非零实数λ、μ,使λ
+μ
=
.
①“数列{an}既是等差数列,又是等比数列”的充要条件是“数列{an}是常数列”;
②不等式|x-1|+|y-1|≤1表示的平面区域是一个菱形及其内部;
③f(x)是(-∞,0)∪(0,+∞)上的奇函数,x>0时的解析式是f(x)=2x,则x<0时的解析式为f(x)=-2-x;
④若两个非零向量
| a |
| b |
| a |
| b |
| 0 |
| A、4 | B、3 | C、2 | D、1 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:①不正确,举例:常数列:0,0,0,…,0,是等差数列,但是不是等比数列;
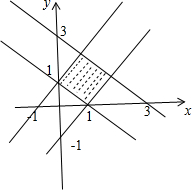
②不等式|x-1|+|y-1|≤1表示的平面区域如图所示,即可判断出正误;
③利用奇函数的定义及其性质,即可判断出正误;
④利用向量共线定理,即可判断出正误.
②不等式|x-1|+|y-1|≤1表示的平面区域如图所示,即可判断出正误;
③利用奇函数的定义及其性质,即可判断出正误;
④利用向量共线定理,即可判断出正误.
解答:
 解:①不正确,举例:常数列:0,0,0,…,0,是等差数列,但是不是等比数列,因此数列{an}既是等差数列,又是等比数列”的必要不充分条件是“数列{an}是常数列”;
解:①不正确,举例:常数列:0,0,0,…,0,是等差数列,但是不是等比数列,因此数列{an}既是等差数列,又是等比数列”的必要不充分条件是“数列{an}是常数列”;
②不等式|x-1|+|y-1|≤1表示的平面区域如图所示:是一个菱形及其内部,正确;
③f(x)是(-∞,0)∪(0,+∞)上的奇函数,x>0时的解析式是f(x)=2x,
则x<0时,-x>0,∴f(x)=-f(-x)=-2-x,因此正确;
④若两个非零向量
、
共线,则存在两个非零实数λ、μ,使λ
+μ
=
,正确.
 解:①不正确,举例:常数列:0,0,0,…,0,是等差数列,但是不是等比数列,因此数列{an}既是等差数列,又是等比数列”的必要不充分条件是“数列{an}是常数列”;
解:①不正确,举例:常数列:0,0,0,…,0,是等差数列,但是不是等比数列,因此数列{an}既是等差数列,又是等比数列”的必要不充分条件是“数列{an}是常数列”;②不等式|x-1|+|y-1|≤1表示的平面区域如图所示:是一个菱形及其内部,正确;
③f(x)是(-∞,0)∪(0,+∞)上的奇函数,x>0时的解析式是f(x)=2x,
则x<0时,-x>0,∴f(x)=-f(-x)=-2-x,因此正确;
④若两个非零向量
| a |
| b |
| a |
| b |
| 0 |
点评:本题考查了等差数列与等比数列的性质、不等式|x-1|+|y-1|≤1表示的平面区域、奇函数的定义及其性质、向量共线定理、简易逻辑的判定,考查了推理能力与计算能力,考查了数形结合的思想方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
将函数f(x)=cos2x的图象向右平移
个单位后得到函数g(x),则g(x)具有性质( )
| π |
| 4 |
A、最大值为a,图象关于直线x=
| ||||
B、在(0,
| ||||
C、在(-
| ||||
D、周期为π,图象关于点(
|
已知两个单位向量
,
的夹角为60°,
=(1-t)
+t
,若
•
=-
,则实数t的取值是( )
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| 1 |
| 2 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
命题p:?x∈N,x3<x2;命题q:?a∈(0,1)∪(1,+∞),函数f(x)=loga(x-1)的图象过点(2,0),则( )
| A、p假q假 | B、p真q假 |
| C、p假q真 | D、p真q真 |
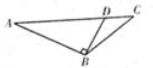
如图,在△ABC中,点D在AC上,AB⊥BD,BC=3
,BD=5,sin∠ABC=
,则CD的长为( )
| 3 |
2
| ||
| 5 |

A、
| ||
| B、4 | ||
C、2
| ||
| D、5 |
数列{an}满足an+1=
,若a1=
,则a2015=( )
|
| 4 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图所示的是正方形的顶点A为圆心,边长为半径的画弧形成的图象,现向正方形内投掷一颗豆子(假设豆子不落在线上),则恰好落在阴影部分的概率为
如图所示的是正方形的顶点A为圆心,边长为半径的画弧形成的图象,现向正方形内投掷一颗豆子(假设豆子不落在线上),则恰好落在阴影部分的概率为