题目内容
已知关于x的一元二次函数f(x)=b2x2-(a+1)x+1.
(Ⅰ)若a,b分别表示将一覆盖质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求y=f(x)恰有一个零点的概率;
(Ⅱ)若a,b∈[1,6],求满足y=f(x)的零点的概率.
(Ⅰ)若a,b分别表示将一覆盖质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求y=f(x)恰有一个零点的概率;
(Ⅱ)若a,b∈[1,6],求满足y=f(x)的零点的概率.
考点:几何概型,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)求出y=f(x)恰有一个零点等价条件,利用古典关系的概率公式即可得到结论;
(Ⅱ)利用几何概型的概率公式即可得到结论.
(Ⅱ)利用几何概型的概率公式即可得到结论.
解答:
解:(Ⅰ)设(a,b)表示一个基本事件,则抛掷两次骰子的所有基本事件有(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),…,(6,5),(6,6),共36个.
用A表示事件“y=f(x)恰有一个零点”,即△=(a+1)2-4b2=0,
则a+1=2b.
则A包含的基本事件有(1,1),(3,2),(5,3),共3个.
∴P(A)=
=
.
答:事件“y=f(x)恰有一个零点”的概率为
.
(Ⅱ)用B表示事件“y=f(x)有零点”,即a+1≥2b.
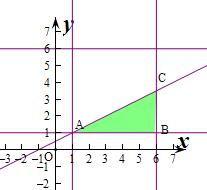
试验的全部结果所构成的区域为{(x,y)|1≤x≤6,1≤y≤6},
构成事件B的区域为{(x,y)|1≤x≤6,1≤y≤6,x-2y+1>0},
所以所求的概率为P(B)=
=
.
答:事件“y=f(x)有零点”的概率为
.
用A表示事件“y=f(x)恰有一个零点”,即△=(a+1)2-4b2=0,
则a+1=2b.
则A包含的基本事件有(1,1),(3,2),(5,3),共3个.
∴P(A)=
| 3 |
| 36 |
| 1 |
| 12 |
答:事件“y=f(x)恰有一个零点”的概率为
| 1 |
| 12 |

(Ⅱ)用B表示事件“y=f(x)有零点”,即a+1≥2b.
试验的全部结果所构成的区域为{(x,y)|1≤x≤6,1≤y≤6},
构成事件B的区域为{(x,y)|1≤x≤6,1≤y≤6,x-2y+1>0},
所以所求的概率为P(B)=
| ||||
| 5×5 |
| 1 |
| 4 |
答:事件“y=f(x)有零点”的概率为
| 1 |
| 4 |
点评:本题主要考查几何概型和古典概型的概率的计算,要求熟练掌握相应的概率公式.

练习册系列答案
相关题目
 高三某班20名男生在一次体检中被平均分成两个小组,第一组和第二组学生身高(单位:cm)的统计数据用茎叶图表示,如图所示.
高三某班20名男生在一次体检中被平均分成两个小组,第一组和第二组学生身高(单位:cm)的统计数据用茎叶图表示,如图所示.