题目内容
函数f(x)=sinωx+
cosωx(x∈R),又f(α)=-2,f(β)=0,且|α-β|的最小值等于π,则正数ω的值为 .
| 3 |
考点:三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:首先,化简函数解析式,然后,根据f(α)=-2,f(β)=0,得到α,β之间的关系,然后,利用|α-β|的最小值等于π,确定正数ω的值.
解答:
解:∵f(x)=sinωx+
cosωx(x∈R),
∴f(x)=2sin(ωx+
),
∵f(α)=-2,
∴f(α)=2sin(ωα+
)=-2,
∴ωα+
=-
+2kπ,k∈Z,
∴α=-
+
,
∵f(β)=0,
∴f(β)=2sin(ωβ+
)=0,
∴ωβ+
=nπ,n∈Z,
∴β=-
+
,
又∵|α-β|=|-
+
+
-
|,
∴|α-β|min=
=π,
∴ω=
故答案为:
.
| 3 |
∴f(x)=2sin(ωx+
| π |
| 3 |
∵f(α)=-2,
∴f(α)=2sin(ωα+
| π |
| 3 |
∴ωα+
| π |
| 3 |
| π |
| 2 |
∴α=-
| 5π |
| 6ω |
| 2kπ |
| ω |
∵f(β)=0,
∴f(β)=2sin(ωβ+
| π |
| 3 |
∴ωβ+
| π |
| 3 |
∴β=-
| π |
| 3ω |
| nπ |
| ω |
又∵|α-β|=|-
| 5π |
| 6ω |
| 2kπ |
| ω |
| π |
| 3ω |
| nπ |
| ω |
∴|α-β|min=
| π |
| 2ω |
∴ω=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题重点考查了二倍角公式、三角恒等变换公式、三角函数的图象与性质等知识,考查运算求解能力,为中档题.

练习册系列答案
相关题目
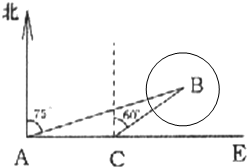 如图,海中有一小岛B,周围3.8海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.
如图,海中有一小岛B,周围3.8海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.