题目内容
4．设全集U=R，集合A={x|x＜0}，B={x||x|＞1}，则A∩（∁UB）={x|-1≤x＜0}．分析 化简集合B，根据补集与交集的定义求出结果即可．
解答 解：全集U=R，集合A={x|x＜0}，
B={x||x|＞1}={x|x＜-1或x＞1}，
则∁UB={x|-1≤x≤1}，
A∩（∁UB）={x|-1≤x＜0}．
故答案为：{x|-1≤x＜0}．
点评 本题考查了集合的定义与运算问题，是基础题目．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
15．已知tanα=2，则$\frac{{2{{sin}^2}α+1}}{{cos2（α-\frac{π}{4}）}}$的值是（ ）
| A． | $\frac{5}{3}$ | B． | $-\frac{13}{4}$ | C． | $\frac{13}{5}$ | D． | $\frac{13}{4}$ |
12．如图，在△ABC中，点D在线段BC上，且BD=2DC，若$\overrightarrow{AD}=λ\overrightarrow{AB}+μ\overrightarrow{AC}$，则$\frac{λ}{μ}$=（ ）
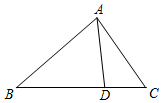
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | 2 | D． | $\frac{2}{3}$ |
13．“a=3”是“直线y=-ax+2与y=$\frac{a}{9}$x-5垂直”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |