题目内容
5.已知正方体ABCD-A1B1C1D1的棱长为1,P是A1C1上任意一点,记平面PAB、平面PBC与下底面所成的二面角分别为α,β,则tan(α+β)的最小值为-$\frac{4}{3}$.分析 连P作PO⊥底面ABCD,过O分别作OM⊥AB,ON⊥BC,则∠PMO=α,∠PNO=β,由此利用二次函数性质能求出能求出tan(α+β)的最小值.
解答 解:连P作PO⊥底面ABCD,过O分别作OM⊥AB,ON⊥BC,
则∠PMO=α,∠PNO=β,
∵PO=1,∴tan$α=\frac{1}{OM}$,tanβ=$\frac{1}{ON}$,
∴tan(α+β)=$\frac{\frac{1}{OM}+\frac{1}{ON}}{1-\frac{1}{OM}•\frac{1}{ON}}$=$\frac{OM+ON}{OM•ON-1}$,
设OA=x,0<x<$\sqrt{2}$,
则tan(α+β)=$\frac{OM+ON}{OM•ON-1}$
=$\frac{\frac{\sqrt{2}}{2}x+\frac{\sqrt{2}}{2}(\sqrt{2}-x)}{\frac{\sqrt{2}}{2}x•\frac{\sqrt{2}}{2}(\sqrt{2}-x)-1}$
=$\frac{1}{\frac{1}{2}x(\sqrt{2}-x)-1}$=$\frac{1}{-\frac{1}{2}({x}^{2}-\sqrt{2}x)-1}$
=$\frac{1}{-\frac{1}{2}(x-\frac{\sqrt{2}}{2})^{2}-\frac{3}{4}}$$≥-\frac{4}{3}$.
∴tan(α+β)的最小值为-$\frac{4}{3}$.
故答案为:-$\frac{4}{3}$.
点评 本题考查两个面面角和的正切值的最小值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
12.在区间[0,π]上随机取一个x,则y=sinx的值在0到$\frac{1}{2}$之间的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{π}$ |
17.${({{x^2}+\frac{1}{x^2}-2})^3}$展开式中的常数项为( )
| A. | 20 | B. | -20 | C. | 15 | D. | -15 |
14.设F为抛物线C:y2=4x的焦点,过F的直线l与C相交于A、B两点,线段AB的垂直平分线交x轴于点M,若|AB|=6,则|FM|的长为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
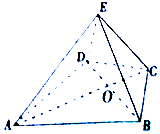 如图,在四棱锥E-ABCD中,△ABD是正三角形,△BCD是等腰三角形,∠BCD=120°,EC⊥BD,连结AC交BD于点O.
如图,在四棱锥E-ABCD中,△ABD是正三角形,△BCD是等腰三角形,∠BCD=120°,EC⊥BD,连结AC交BD于点O.