题目内容
15.已知f(x)=ax-lnx,x∈(0,e],g(x)=$\frac{lnx}{x}$,其中e是自然对数的底数,a∈R.(Ⅰ)当a=1时,求函数f(x)的单调区间和极值;
(Ⅱ)求证:在(Ⅰ)的条件下,f(x)>g(x)+$\frac{1}{2}$;
(Ⅲ)是否存在实数a,使f(x)的最小值是3,若存在,求出a的值;若不存在,请说明理由.
分析 (Ⅰ)当a=1时,求函数的定义域,然后利用导数求函数的极值和单调性.
(Ⅱ)利用(Ⅰ)的结论,求函数f(x)的最小值以及g(x)的最大值,利用它们之间的关系证明不等式.
(Ⅲ)利用导数求函数的最小值,让最小值等于3,解参数a.
解答 解:(Ⅰ)因为f(x)=x-lnx,f′(x)=1-$\frac{1}{x}$=$\frac{x-1}{x}$,
所以当0<x<1时,f'(x)<0,此时函数f(x)单调递减,
当1<x≤e时,f'(x)>0,此时函数f(x)单调递增,
所以函数f(x)的极小值为f(1)=1.
(Ⅱ)证明:因为函数f(x)的极小值为1,即函数f(x)在(0,e]上的最小值为1.
又g′(x)=$\frac{1-lnx}{{x}^{2}}$,所以当0<x<e时,g'(x)>0,此时g(x)单调递增.
所以g(x)的最大值为g(e)=$\frac{1}{e}$<$\frac{1}{2}$,所以f(x)min-g(x)max>$\frac{1}{2}$,
所以在(Ⅰ)的条件下,f(x)>g(x)+$\frac{1}{2}$.
(Ⅲ)假设存在实数a,使f(x)=ax-lnx,x∈(0,e],有最小值3,
则f′(x)=a-$\frac{1}{x}$=$\frac{ax-1}{x}$,
①当a≤0时,f'(x)<0,f(x)在(0,e]上单调递减,
f(x)min=f(e)=ae-1=3,a=$\frac{4}{e}$,(舍去),此时函数f(x)的最小值不是3.
②当0<$\frac{1}{a}$<e时,f(x)在(0,$\frac{1}{a}$]上单调递减,f(x)在($\frac{1}{a}$,e]上单调递增.
所以f(x)min=f($\frac{1}{a}$)=1+lna=3,a=e2,满足条件.
③当$\frac{1}{a}$≥e时,f(x)在(0,e]上单调递减,
f(x)min=f(e)=ae-1=3,a=$\frac{4}{e}$,(舍去),
此时函数f(x)的最小值是3,
综上可知存在实数a=e2,使f(x)的最小值是3.
点评 本题主要考查利用函数的单调性研究函数的单调性问题,运算量较大,综合性较强.

| A. | $\frac{3}{2}$ | B. | 1 | C. | 2 | D. | 3 |
| A. | 8 | B. | 8$\sqrt{2}$ | C. | 16 | D. | 16$\sqrt{2}$ |
| 车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
| 限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
(2)设X表示该公司在星期二和星期三两天出车的车辆数之和,求X的分布列及数学期望.
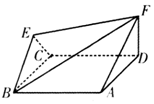 如图,菱形ABCD与正三角形BCE的边长均为2,且平面ABCD⊥平面BCE,FD⊥平面ABCD,$FD=\sqrt{3}$.
如图,菱形ABCD与正三角形BCE的边长均为2,且平面ABCD⊥平面BCE,FD⊥平面ABCD,$FD=\sqrt{3}$.