题目内容
12.在区间[0,π]上随机取一个x,则y=sinx的值在0到$\frac{1}{2}$之间的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{π}$ |
分析 解出关于三角函数的不等式,使得在区间[0,π]上,y=sinx的值在0到$\frac{1}{2}$之间,在所给的范围中,求出符合条件的角的范围,根据几何概型公式用角度之比求解概率.
解答 解:在区间[0,π]上,y=sinx的值在0到$\frac{1}{2}$之间,则x∈[0,$\frac{π}{6}$]∪[$\frac{5π}{6}$,π],区间长度为$\frac{π}{3}$,
∴在区间[0,π]上随机取一个x,y=sinx的值在0到$\frac{1}{2}$之间的概率为$\frac{\frac{π}{3}}{π-0}$=$\frac{1}{3}$,
故选B.
点评 本题主要考查了几何概型.古典概型和几何概型是我们学习的两大概型,在解题过程中不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、和体积的比值得到.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
2.平面向量$\overrightarrow a$与$\overrightarrow b$的夹角为$\frac{2π}{3}$,$\overrightarrow a=(2,0)$,$|\overrightarrow b|=1$,则$|\overrightarrow a+2\overrightarrow b|$=( )
| A. | 1 | B. | 2 | C. | $2\sqrt{3}$ | D. | 4 |
7.某公司有A,B,C,D,E五辆汽车,其中A、B两辆汽车的车牌尾号均为1,C、D两辆汽车的车牌尾号均为2,E车的车牌尾号为6,已知在非限行日,每辆车可能出车或不出车,A、B、E三辆汽车每天出车的概率均为$\frac{1}{2}$,C、D两辆汽车每天出车的概率均为$\frac{2}{3}$,且五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
(1)求该公司在星期一至少有2辆汽车出车的概率;
(2)设X表示该公司在星期二和星期三两天出车的车辆数之和,求X的分布列及数学期望.
| 车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
| 限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
(2)设X表示该公司在星期二和星期三两天出车的车辆数之和,求X的分布列及数学期望.
2.已知角α的终边经过点(3a-9,a+2),且sin2α≤0,sinα>0,则a的取值范围是( )
| A. | (-2,3) | B. | [-2,3) | C. | (-2,3] | D. | [-2,3] |
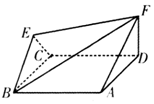 如图,菱形ABCD与正三角形BCE的边长均为2,且平面ABCD⊥平面BCE,FD⊥平面ABCD,$FD=\sqrt{3}$.
如图,菱形ABCD与正三角形BCE的边长均为2,且平面ABCD⊥平面BCE,FD⊥平面ABCD,$FD=\sqrt{3}$.