题目内容
14.设F为抛物线C:y2=4x的焦点,过F的直线l与C相交于A、B两点,线段AB的垂直平分线交x轴于点M,若|AB|=6,则|FM|的长为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
分析 先根据抛物线方程求出p的值,再由抛物线的性质求出AB的垂直平分线方程,可得到答案.
解答 解:∵抛物线y2=4x,∴p=2,
设经过点F的直线y=k(x-1)与抛物线相交于A、B两点,A(x1,y1),B(x2,y2),
直线y=k(x-1)代入y2=4x,整理可得k2x2-(2k2+4)x+k2=0,
∴x1+x2=2+$\frac{4}{{k}^{2}}$
利用抛物线定义,AB中点横坐标为x1+x2=|AB|-p=6-2=4.AB中点横坐标为2
∴2+$\frac{4}{{k}^{2}}$=4,∴k=±$\sqrt{2}$
AB中点纵坐标为k,AB的垂直平分线方程为y-k=-$\frac{1}{k}$(x-2),
令y=0,可得x=4,
∴|FM|=3.
故选:D.
点评 本题主要考查了抛物线的性质.属中档题.解题时要认真审题,仔细解答,注意等价转化思想的合理运用,确定AB的垂直平分线方程是关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
2.已知角α的终边经过点(3a-9,a+2),且sin2α≤0,sinα>0,则a的取值范围是( )
| A. | (-2,3) | B. | [-2,3) | C. | (-2,3] | D. | [-2,3] |
9.已知双曲线$\frac{x^2}{6}-\frac{y^2}{3}=1$的焦点为F1、F2,点M在双曲线上且MF1⊥F1F2,则F1到直线MF2的距离为( )
| A. | $\frac{{3\sqrt{6}}}{5}$ | B. | $\frac{{5\sqrt{6}}}{6}$ | C. | $\frac{6}{5}$ | D. | $\frac{5}{6}$ |
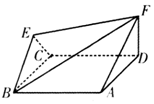 如图,菱形ABCD与正三角形BCE的边长均为2,且平面ABCD⊥平面BCE,FD⊥平面ABCD,$FD=\sqrt{3}$.
如图,菱形ABCD与正三角形BCE的边长均为2,且平面ABCD⊥平面BCE,FD⊥平面ABCD,$FD=\sqrt{3}$.