题目内容
13.已知数列{an}的前n项和Sn=n2+n,a1=2.(1)求数列{an}的通项公式;
(2)求数列{an-3×5-n}的前n项和Tn.
分析 (1)利用公式an=Sn-Sn-1求出通项公式,再验证n=1即可;
(2)将Tn分成等差数列的前n项和与等比数列的前n项和,利用求和公式计算.
解答 解:(1)当n≥2时,an=Sn-Sn-1=n2+n-[(n-1)2+(n-1)]=2n,
经检验,当n=1时,上式成立,
∴an=2n.
(2)Tn=2-$\frac{3}{5}$+4-$\frac{3}{{5}^{2}}$+6-$\frac{3}{{5}^{3}}$+…+2n-$\frac{3}{{5}^{n}}$
=(2+4+6+…+2n)-($\frac{3}{5}+\frac{3}{{5}^{2}}+\frac{3}{{5}^{3}}$+…+$\frac{3}{{5}^{n}}$)
=$\frac{2+2n}{2}•n$-$\frac{\frac{3}{5}[1-(\frac{1}{5})^{n}]}{1-\frac{1}{5}}$
=n(n+1)-$\frac{3}{4}$(1-$\frac{1}{{5}^{n}}$).
点评 本题考查了通项公式的求法,等差数列,等比数列的前n项和公式,属于中档题.

练习册系列答案
相关题目
18.下列函数中,在区间(0,+∞)上为增函数的是( )
| A. | f(x)=x2+3x | B. | y=(x-1)2 | C. | g(x)=2-x | D. | y=log0.5(x+1) |
5.若函数y=f(x+1)是偶函数,则函数y=f(x)的图象的对称轴方程是( )
| A. | x=1 | B. | x=-1 | C. | x=2 | D. | x=-2 |
2.如果直线l1:ax+2y+6=0与直线l2:x+(a-1)y+3=0垂直,那么a等于( )
| A. | 2 | B. | -1 | C. | -1或2 | D. | $\frac{2}{3}$ |
13.已知过点A(-2,m)和B(m,4)的直线与直线y=2x+1平行,则m=( )
| A. | 0 | B. | -8 | C. | 2 | D. | 10 |
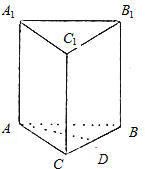 如图,在直三棱柱ABC-A1B1C1中,AB=BC=AC=AA1=1,D是BC的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=AC=AA1=1,D是BC的中点.