题目内容
8.已知数列{an}满足a1=1,其前n项和是Sn对任意正整数n,Sn=n2an,求此数列的通项公式.分析 由Sn=n2an,可得n≥2时,an=Sn-Sn-1,化为:$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n-1}{n+1}$.利用“累乘求积”方法即可得出.
解答 解:∵Sn=n2an,∴n≥2时,an=Sn-Sn-1=n2an-(n-1)2an-1,化为:$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n-1}{n+1}$.
∴an=$\frac{{a}_{n}}{{a}_{n-1}}$•$\frac{{a}_{n-1}}{{a}_{n-2}}$$•\frac{{a}_{n-2}}{{a}_{n-3}}$•…•$\frac{{a}_{3}}{{a}_{2}}$$•\frac{{a}_{2}}{{a}_{1}}$•a1=$\frac{n-1}{n+1}$$•\frac{n-2}{n}$•$\frac{n-3}{n-1}$•…•$\frac{2}{4}$×$\frac{1}{3}$×1
=$\frac{2}{n(n+1)}$,n=1时也成立.
∴an=$\frac{2}{n(n+1)}$.
点评 本题考查了数列递推关系、“累乘求积”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
16.一个容量为10的样本数据,分组后,组距与频数如下:
则样本落在区间(-∞,5]的频率是$\frac{7}{10}$.
| 组距 | (1,2] | (2,3] | (3,4] | (4,5] | (5,6] | (6,7] |
| 频数 | 1 | 1 | 2 | 3 | 1 | 2 |
8.设函数f(x)=$\left\{\begin{array}{l}{{x}^{-1},x≤a}\\{{x}^{-2},x>a}\end{array}\right.$,其中a≠0,若存在实数b,使得函数g(x)=f(x)-b有两个零点,则a的取值范围是( )
| A. | (0,1) | B. | (-∞,0)∪(0,1) | C. | (-∞,0)∪(0,2) | D. | (-1,0)∪(0,1) |
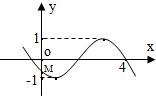 已知函数f(x)=Asin(ωx+φ)(x∈R),且A>0,ω>0,-π≤φ≤0.若f(x)的部分图象如图,且与y轴交点M(0,-$\frac{{\sqrt{2}}}{2}$),则ω+φ=-$\frac{5π}{16}$.
已知函数f(x)=Asin(ωx+φ)(x∈R),且A>0,ω>0,-π≤φ≤0.若f(x)的部分图象如图,且与y轴交点M(0,-$\frac{{\sqrt{2}}}{2}$),则ω+φ=-$\frac{5π}{16}$.