题目内容
已知二次函数f（x）=x2-2ax+2，x∈[0，3]，求f（x）的最小值．
考点：二次函数的性质
专题：分类讨论,函数的性质及应用
分析：讨论a的取值，判断f（x）在x∈[0，3]的单调性，求出f（x）的最小值即可．
解答：
解：∵二次函数f（x）=x2-2ax+2=（x-a）2+2-a2，
且x∈[0，3]，
∴当a∈[0，3]时，f（x）在x∈[0，3]上先减后增，
f（x）的最小值是f（a）=2-a2；
当a∈（-∞，0）时，f（x）在[0，3]上是增函数，
f（x）的最小值是f（0）=2；
当a∈（3，+∞）时，f（x）在[0，3]上是减函数，
f（x）的最小值是f（3）=11-6a；
综上，a∈[0，3]时，f（x）的最小值是2-a2；
a∈（-∞，0）时，f（x）的最小值是2；
a∈（3，+∞）时，f（x）的最小值是11-6a．
且x∈[0，3]，
∴当a∈[0，3]时，f（x）在x∈[0，3]上先减后增，
f（x）的最小值是f（a）=2-a2；
当a∈（-∞，0）时，f（x）在[0，3]上是增函数，
f（x）的最小值是f（0）=2；
当a∈（3，+∞）时，f（x）在[0，3]上是减函数，
f（x）的最小值是f（3）=11-6a；
综上，a∈[0，3]时，f（x）的最小值是2-a2；
a∈（-∞，0）时，f（x）的最小值是2；
a∈（3，+∞）时，f（x）的最小值是11-6a．
点评：本题考查了分类讨论思想的应用问题，也考查了二次函数的图象与性质的应用问题，是基础题目．
练习册系列答案
阅读快车系列答案
相关题目
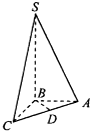如图，在四面体S-ABC中，AB，BC，BS两两垂直，且AB=BC=2，BS=4，点D为AC的中点．若异面直线AS与BD所成角为θ，则cosθ的值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、-
|