题目内容
已知集合M={0，1，2，3，4，5}，P（a，b）表示平面上的点，a、b∈M．
（1）P可以表示平面上的多少个不同点
（2）P可以表示多少个不在直线y=x上的点？
（1）P可以表示平面上的多少个不同点
（2）P可以表示多少个不在直线y=x上的点？
考点：计数原理的应用
专题：排列组合
分析：（1）从集合M中，第一次取一个为横坐标，第二次再取一个为纵坐标，根据分步计数原理即可得到答案．
（2）若P点在直线y=x上，则a=b，列举即可．
（2）若P点在直线y=x上，则a=b，列举即可．
解答：
解：（1）从集合M中，第一次取一个为横坐标，第二次再取一个为纵坐标，共有6×6=36种；
（2）若P点在直线y=x上，则有（0，0），（1，1），（2，2），（3，3），（4，4），（5，5）共6种．
（2）若P点在直线y=x上，则有（0，0），（1，1），（2，2），（3，3），（4，4），（5，5）共6种．
点评：本题考查了分步计数原理，属于基础题．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
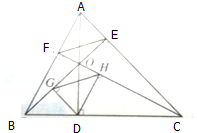如图所示，已知AD，BE，CF是△ABC的三条高，DG⊥BE于点G，DH⊥CF于点H，求证：HG∥EF．