题目内容
19.已知函数f(x)是二次函数,且满足f(0)=1,f(x+1)-f(x)=2x+5;函数g(x)=ax(a>0且a≠1)(1)求f(x)的解析式;
(2)若g(2)=$\frac{1}{4}$,且g[f(x)]≥k对x∈[-1,1]恒成立,求实数k的取值范围.
分析 (1)利用关系式求出f(1),f(2),利用待定系数法求出f(x);
(2)求出a的值,判断g(f(x))的单调性,根据单调性得出g(f(x))在[-1,1]上的最小值,从而得出k的范围.
解答 解:(1)∵f(x+1)-f(x)=2x+5,
∴f(1)-f(0)=5,f(2)-f(1)=7,
又f(0)=1,∴f(1)=6,f(2)=13.
设f(x)=mx2+bx+c,
则$\left\{\begin{array}{l}{c=1}\\{m+b+c=6}\\{4m+2b+c=13}\end{array}\right.$,解得m=1,b=4.
∴f(x)=x2+4x+1.
(2)∵g(2)=a2=$\frac{1}{4}$,∴a=$\frac{1}{2}$.
∴g[f(x)]=($\frac{1}{2}$)${\;}^{{x}^{2}+4x+1}$,
∵f(x)=x2+4x+1在[-1,1]上单调递增,g(x)是减函数,
∴g(f(x))在[-1,1]上是减函数,
g(f(x))在[-1,1]上的最小值为g(f(1))=g(6)=$\frac{1}{{2}^{6}}$=$\frac{1}{64}$.
∵g[f(x)]≥k对x∈[-1,1]恒成立,
∴k≤$\frac{1}{64}$.
点评 本题考查了二次函数的性质,函数最值与恒成立问题,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.设函数$f(x)=\left\{\begin{array}{l}lnx,x≥1\\ f(\frac{1}{x}),0<x<1\end{array}\right.$,则f(f(e-2))=ln2.
7.(x-1)($\frac{1}{x}$+x)6的展开式中的一次项系数是( )
| A. | 5 | B. | 14 | C. | 20 | D. | 35 |
14.某几何体三视图如图,则该几何体的外接球的表面积是( )


| A. | 7π | B. | $\frac{25π}{2}$ | C. | 12π | D. | 25π |
4.m,n是不同的直线,α,β是不重合的平面,下列说法正确的是( )
| A. | 若α∥β,m?α,n?β,则m∥n | |
| B. | 若m,n?α,m∥β,n∥β,则α∥β | |
| C. | m,n是异面直线,若m∥α,m∥β,n∥α,n∥β,则α∥β | |
| D. | 若α∥β,m∥α,则m∥β |
8.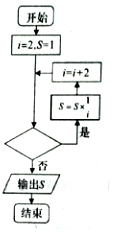 如图,给出的是计算连乘数值的程序框图,其中判断框内不能填入( )
如图,给出的是计算连乘数值的程序框图,其中判断框内不能填入( )
 如图,给出的是计算连乘数值的程序框图,其中判断框内不能填入( )
如图,给出的是计算连乘数值的程序框图,其中判断框内不能填入( )| A. | i≤2019? | B. | i<2019? | C. | i≤2017? | D. | i≤2018? |