题目内容
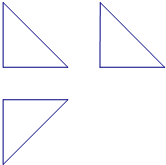如图，某三棱锥的三视图都是直角边为| 2 |
A、
| ||
| B、6π | ||
C、2
| ||
| D、8π |
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由三视图可得几何体是三棱锥，即正方体的一个角，根据三视图的数据，求出三棱锥的外接球的半径和表面积即可．
解答：
解：由三视图可知：该几何体为三棱锥，
由题意得，PA⊥平面ABC，AC⊥AB，则PA=AC=AB=
，
且∠PAC=∠PAB=∠CAB=90°，
所以它是棱长为
的正方体的一个角，
即它的外接球就是棱长为
的正方体的外接球，
则接球的半径R=
=
，
所以该三棱锥的外接球的表面积是S=4πR2=6π，
故选：B．
由题意得，PA⊥平面ABC，AC⊥AB，则PA=AC=AB=
| 2 |
且∠PAC=∠PAB=∠CAB=90°，
所以它是棱长为
| 2 |
即它的外接球就是棱长为
| 2 |
则接球的半径R=
| 1 |
| 2 |
| 3×2 |
| ||
| 2 |
所以该三棱锥的外接球的表面积是S=4πR2=6π，
故选：B．
点评：本题考查由三视图还原直观图形，球的表面积公式，以及三棱锥的外接球转化正方体外接球问题，考查了转化思想．
练习册系列答案
名校课堂系列答案
相关题目
函数y=sin（2x+
）图象的一条对称轴方程为（ ）
| π |
| 2 |
A、x=-
| ||
B、x=-
| ||
C、x=
| ||
D、x=
|
若a＞0，b＞0，a+b=1，则y=
+
的最小值是（ ）
| 1 |
| a |
| 1 |
| b |
| A、2 | B、3 | C、4 | D、5 |
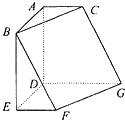如图，在六面体ABCDEFG中，平面ABC∥平面DEFG，AD⊥平面DEFG，AB⊥AC，ED⊥DG，