题目内容
下列说法：
①任何一个几何体都必须有顶点、棱和面；
②一个几何体可以没有顶点；
③一个几何体可以没有棱；
④一个几何体可以没有面．
其中正确的个数是（ ）
①任何一个几何体都必须有顶点、棱和面；
②一个几何体可以没有顶点；
③一个几何体可以没有棱；
④一个几何体可以没有面．
其中正确的个数是（ ）
| A、1 | B、2 | C、3 | D、4 |
考点：旋转体（圆柱、圆锥、圆台）,命题的真假判断与应用
专题：规律型
分析：如果我们只考虑一个物体占有空间部分的形状和大小，而不考虑其他因素，则这个空间部分叫做一个几何体．
解答：
解：如果我们只考虑一个物体占有空间部分的形状和大小，而不考虑其他因素，则这个空间部分叫做一个几何体．故根据几何体的定义，可知球没有顶点，有面，没有棱，故①④不正确，②③正确．
故选：B．
故选：B．
点评：本题考查几何体的概念，考查学生对概念的理解，属于基础题．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
已知全集U={-2，-1，0，1，2，3，4，5，6}，集合M={大于-1且小于4的整数}，则∁UM=（ ）
| A、∅ |
| B、{-2，-1，5，6} |
| C、{0，1，2，3，4} |
| D、{-2，-1，4，5，6} |
已知双曲线
-
=1(a＞0，b＞0)的左右焦点分别为F1，F2，点O为坐标原点，点P在双曲线右支上，△PF1F2内切圆的圆心为Q，圆Q与x轴相切于点A，过F2作直线PQ的垂线，垂足为B，则|OA|与|OB|的长度依次为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、a，a | ||||
B、a，
| ||||
C、
| ||||
D、
|
在区间[-2，3]上任取一个数a，则函数f（x）=x2-2ax+a+2有零点的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知中心在原点的双曲线，其右焦点为F（3，0），且F到其中一条渐近线的距离为
，则该双曲线的方程为（ ）
| 5 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
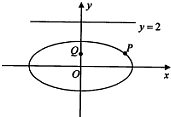已知椭圆C：