题目内容
在平面直角坐标系中,定义d(P,Q)=|x1-x2|+|y1-y2|为P(x1,y1),Q(x2,y2)两点之间的“折线距离”,则椭圆
+y2=1上一点P与直线3x+4y-12=0上一点Q的“折线距离”的最小值为 .
| x2 |
| 2 |
考点:椭圆的简单性质
专题:综合题,新定义,圆锥曲线的定义、性质与方程
分析:根据新定义,利用参数法,表示出椭圆
+y2=1上一点P与直线3x+4y-12=0上一点Q的“折线距离”,然后分类讨论求出最小值.
| x2 |
| 2 |
解答:
解:设直线3x+4y-12=0上的任意一点坐标(x,3-
x),椭圆
+y2=1上任意一点的坐标为(
cosθ,sinθ)
由题意可知:d=|x-
cosθ|+|3-
x-sinθ|
分类讨论:
①x≥4-
sinθ,d=x-
cosθ-3+
x+sinθ=
x-3-
cosθ+sinθ≥4-
cosθ-
sinθ
=4-
sin(θ+α)≥
②4-
sinθ>x>
cosθ解同上
③x≤
cosθ,d=-(x-
cosθ-3+
x+sinθ)=-(
x-3-
cosθ+sinθ)≥-
cosθ-sinθ+3
=3+
sin(θ+β)≥
.
∴椭圆
+y2=1上一点P与直线3x+4y-12=0上一点Q的“折线距离”的最小值为
.
故答案为:
.
| 3 |
| 4 |
| x2 |
| 2 |
| 2 |
由题意可知:d=|x-
| 2 |
| 3 |
| 4 |
分类讨论:
①x≥4-
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 7 |
| 4 |
| 2 |
| 2 |
| 4 |
| 3 |
=4-
| ||
| 3 |
12-
| ||
| 3 |
②4-
| 4 |
| 3 |
| 2 |
③x≤
| 2 |
| 2 |
| 3 |
| 4 |
| 7 |
| 4 |
| 2 |
3
| ||
| 4 |
=3+
| ||
| 4 |
12-
| ||
| 4 |
∴椭圆
| x2 |
| 2 |
12-
| ||
| 4 |
故答案为:
12-
| ||
| 4 |
点评:本题是中档题,考查新定义,利用新定义求出函数的最小值问题,考查计算能力,对新定义的理解和灵活运应是解好本题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
航空母舰“辽宁舰”在某次舰载机起降飞行训练中,有5架歼-15飞机准备着舰.如果甲、乙两机必须相邻着舰,而甲、丁两机不能相邻着舰,那么不同的着舰方法有( )
| A、12种 | B、16种 |
| C、24种 | D、36种 |
若
,
是夹角为60°的单位向量,则
=2
+
,
=3
+2
的夹角为( )
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
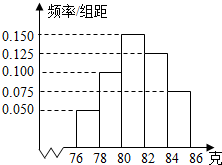 某厂对一批产品进行抽样检测,图2是抽检产品净重(单位:克)数据的频率分布直方图,样本数据分组为[76,78)、[78,80)、…、[84,86].若这批产品有120个,估计其中净重大于或等于78克且小于84克的产品的个数是
某厂对一批产品进行抽样检测,图2是抽检产品净重(单位:克)数据的频率分布直方图,样本数据分组为[76,78)、[78,80)、…、[84,86].若这批产品有120个,估计其中净重大于或等于78克且小于84克的产品的个数是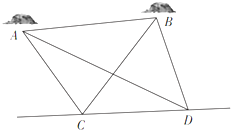 如图,A,B是海平面上的两个小岛,为测量A,B两岛间的距离,测量船以15海里/小时的速度沿既定直线CD航行,在t1时刻航行到C处,测得∠ACB=75°,∠ACD=120°,1小时后,测量船到达D处,测得∠ADC=30°,∠ADB=45°,求A,B两小岛间的距离.(注:A、B、C、D四点共面)
如图,A,B是海平面上的两个小岛,为测量A,B两岛间的距离,测量船以15海里/小时的速度沿既定直线CD航行,在t1时刻航行到C处,测得∠ACB=75°,∠ACD=120°,1小时后,测量船到达D处,测得∠ADC=30°,∠ADB=45°,求A,B两小岛间的距离.(注:A、B、C、D四点共面)