题目内容
(2015•赤峰模拟)某茶楼有四类茶饮,假设为顾客准备泡茶工具所需的时间互相独立,且都是整数分钟,经统计以往为100位顾客准备泡茶工具所需的时间(t),结果如下:
注:服务员在准备泡茶工具时的间隔时间忽略不计,并将频率视为概率.
(1)求服务员恰好在第6分钟开始准备第三位顾客的泡茶工具的概率;
(2)用X表示至第4分钟末已准备好了工具的顾客人数,求X的分布列及数学期望.
| 类别 | 铁观音 | 龙井 | 金骏眉 | 大红袍 |
| 顾客数(人) | 20 | 30 | 40 | 10 |
| 时间t(分钟/人) | 2 | 3 | 4 | 6 |
(1)求服务员恰好在第6分钟开始准备第三位顾客的泡茶工具的概率;
(2)用X表示至第4分钟末已准备好了工具的顾客人数,求X的分布列及数学期望.
考点:离散型随机变量的期望与方差,几何概型,离散型随机变量及其分布列
专题:概率与统计
分析:(1)设Y表示服务员准备工具所需的时间,用P表示对应的概率,求出Y的分布列,由此能求出“服务员在第6分钟开始为第三位顾客准备泡茶工具”的概率.
(2)分析得X的可能取值为0,1,2,求出相应的概率能求出X的分布列与数学期望.
(2)分析得X的可能取值为0,1,2,求出相应的概率能求出X的分布列与数学期望.
解答:
解:(1)设Y表示服务员准备工具所需的时间,用P表示概率,得Y的分布列如下;
A表示事件“服务员在6分钟开始为第三位顾客准备泡茶工具”,则事件A对应两种情形:
①为第一位顾客准备泡茶工具所需的时间为2分钟,且为第二位所需的时间为3分钟;
②为第一位顾客所需的时间为3分钟,且为第一位顾客准备所需的时间为2分钟;
∴P(A)=P(Y=2)•P(Y=3)+P(Y=3)•P(Y=2)
=
×
+
×
=
.
(2)X的取值为0、1、2,
X=0时对应为第一位顾客准备所需的时间超过4分钟,
∴P(X=0)=P(Y>4)=
;
X=1对应为第一位顾客所需的时间2分钟且为第二位顾客准备所需的时间超过2分钟,
或为第一位顾客准备所需的时间3分钟或为第一位顾客准备所需的时间4分钟,
∴P(X=1)=P(Y=2)•P(Y>2)+P(Y=3)+P( Y=4)
=
×
+
+
=
,
X=2对应准备两位顾客泡茶工具的时间均为2分钟,
∴P(X=2)=P(Y=2)P(Y=2)=
×
=
,
∴X的分布列为:
∴X的数学期望是E(X)=0×
+1×
+2×
=
.
| Y | 2 | 3 | 4 | 6 | ||||||||
| P |
|
|
|
|
①为第一位顾客准备泡茶工具所需的时间为2分钟,且为第二位所需的时间为3分钟;
②为第一位顾客所需的时间为3分钟,且为第一位顾客准备所需的时间为2分钟;
∴P(A)=P(Y=2)•P(Y=3)+P(Y=3)•P(Y=2)
=
| 1 |
| 5 |
| 3 |
| 10 |
| 3 |
| 10 |
| 1 |
| 5 |
| 3 |
| 25 |
(2)X的取值为0、1、2,
X=0时对应为第一位顾客准备所需的时间超过4分钟,
∴P(X=0)=P(Y>4)=
| 1 |
| 10 |
X=1对应为第一位顾客所需的时间2分钟且为第二位顾客准备所需的时间超过2分钟,
或为第一位顾客准备所需的时间3分钟或为第一位顾客准备所需的时间4分钟,
∴P(X=1)=P(Y=2)•P(Y>2)+P(Y=3)+P( Y=4)
=
| 1 |
| 5 |
| 4 |
| 5 |
| 3 |
| 10 |
| 2 |
| 5 |
| 43 |
| 50 |
X=2对应准备两位顾客泡茶工具的时间均为2分钟,
∴P(X=2)=P(Y=2)P(Y=2)=
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 25 |
∴X的分布列为:
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 1 |
| 10 |
| 43 |
| 50 |
| 1 |
| 25 |
| 47 |
| 50 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.

练习册系列答案
相关题目
定义域和值域均为[-a,a](常数a>0)的函数y=f(x)和y=g(x)的图象如图所示,给出下列四个命题: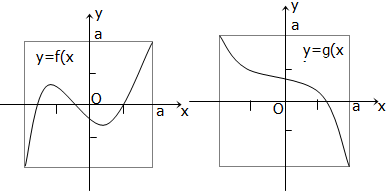
(1)方程f[g(x)]=0有且仅有三个解;
(2)方程g[f(x)]=0有且仅有三个解;
(3)方程f[f(x)]=0有且仅有九个解;
(4)方程g[g(x)]=0有且仅有一个解.
那么,其中正确命题的个数是( )

(1)方程f[g(x)]=0有且仅有三个解;
(2)方程g[f(x)]=0有且仅有三个解;
(3)方程f[f(x)]=0有且仅有九个解;
(4)方程g[g(x)]=0有且仅有一个解.
那么,其中正确命题的个数是( )
| A、(1)(4) |
| B、(2)(3) |
| C、(1)(3) |
| D、(2)(4) |
 ,70),[70,80),[80,90),[90,100].
,70),[70,80),[80,90),[90,100].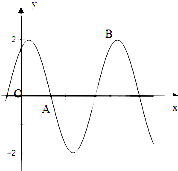 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,图象与x轴交点A及图象最高点B的坐标分别是A(
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,图象与x轴交点A及图象最高点B的坐标分别是A(