题目内容
已知（2-
x）50=a0+a1x+a2x2+…+a50x50，其中a0，a1，…a50是常数，计算：
（1）a0+a1+a2+…+a50；
（2）a0+a2+…+a50；
（3）a10；
（4）（a0+a2+a4+…+a50）2-（a1+a3+…+a49）2．
| 3 |
（1）a0+a1+a2+…+a50；
（2）a0+a2+…+a50；
（3）a10；
（4）（a0+a2+a4+…+a50）2-（a1+a3+…+a49）2．
考点：二项式定理的应用,二项式系数的性质
专题：二项式定理
分析：（1）在所给的二项展开式中，令x=1，即可求得a0+a1+a2+…+a50 的值．
（2）在所给的二项展开式中，令x=1，即可求得a0-a1+a2 -a3+…+a50 的值．
（3）a10 即（2-
x）50的展开式中x10的系数，再利用通项公式求得 a10 的值．
（4）把（1）、（2）得到的等式相乘可得 （a0+a2+a4+…+a50）2-（a1+a3+…+a49）2 =（2-
）50 •（2+
）50=[(2-
)(2+
)]50，计算可得结果．
（2）在所给的二项展开式中，令x=1，即可求得a0-a1+a2 -a3+…+a50 的值．
（3）a10 即（2-
| 3 |
（4）把（1）、（2）得到的等式相乘可得 （a0+a2+a4+…+a50）2-（a1+a3+…+a49）2 =（2-
| 3 |
| 3 |
| 3 |
| 3 |
解答：
解：（1）在（2-
x）50=a0+a1x+a2x2+…+a50x50 中，令x=1，可得a0+a1+a2+…+a50 =（2-
）50 ①．
（2）在（2-
x）50=a0+a1x+a2x2+…+a50x50 中，令x=-1，可得a0-a1+a2 -a3+…+a50 =（2+
）50 ②，
把①、②相加并处以2，求得a0+a2+…+a50 =
③．
（3）a10 即（2-
x）50的展开式中x10的系数，∴a10=
•240•(-
)10．
（4）把①、②相乘可得，（a0+a2+a4+…+a50）2-（a1+a3+…+a49）2 =（2-
）50 •（2+
）50=[(2-
)(2+
)]50=1．
| 3 |
| 3 |
（2）在（2-
| 3 |
| 3 |
把①、②相加并处以2，求得a0+a2+…+a50 =
(2-
| ||||
| 2 |
（3）a10 即（2-
| 3 |
| C | 10 50 |
| 3 |
（4）把①、②相乘可得，（a0+a2+a4+…+a50）2-（a1+a3+…+a49）2 =（2-
| 3 |
| 3 |
| 3 |
| 3 |
点评：本题主要考查二项式定理的应用，在二项展开式中，通过给变量赋值，求得某些项的系数和，是一种简单有效的方法，属于基础题．
练习册系列答案
相关题目
已知幂函数f（x）过点（
，2
），则函数f（x）的表达式为（ ）
| 2 |
| 2 |
A、f（x）=
| ||
| B、f（x）=x2 | ||
| C、f（x）=x3 | ||
D、f（x）=x
|
在正方体ABCD-A1B1C1D1中，O是AC的中点，E是线段D1O上一点，且D1E=2EO．求证平面CDE⊥平面CD1O．
如图所示，F1、F2分别为椭圆C：
如图，在棱长为1的正方体ABCD-A1B1C1D1中．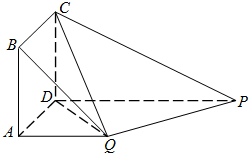
在如图所示的多面体中，四边形ABCD为正方形，四边形ADPQ是直角梯形，AD⊥DP，CD⊥平面ADPQ，AB=AQ=