��Ŀ����
ijͬѧ��һ���о���ѧϰ�з��֣��������ʽ�ӵ�ֵ������ͬһ��������
��sin213�㣫cos217�㣭sin13��cos17�㣻
��sin215�㣫cos215�㣭sin15��cos15�㣻
��sin218�㣫cos212�㣭sin18��cos12�㣻
��sin2(��18��)��cos248�㣭sin(��18��)cos48�㣻
��sin2(��25��)��cos255�㣭sin(��25��)cos55��.
(1)�Դ��������ʽ����ѡ��һ����������������
(2)����(1)�ļ�����������ͬѧ�ķ����ƹ�Ϊ���Ǻ��ʽ����֤����Ľ��ۣ�
�ⷨ1��(1)ѡ���ʽ���������£�
sin215�㣫cos215�㣭sin15��cos15��
��1��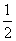 sin30�㣽1��
sin30�㣽1�� ��
�� .
.
(2)���Ǻ��ʽΪsin2����cos2(30�㣭��)��sin��cos(30�㣭��)�� .
.
֤�����£�
sin2����cos2(30�㣭��)��sin��cos(30�㣭��)
��sin2����(cos30��cos����sin30��sin��)2��sin��(cos30��cos����sin30��sin��)
��sin2���� cos2����
cos2���� sin��cos����
sin��cos���� sin2����
sin2���� sin��cos����
sin��cos����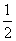 sin2����
sin2���� sin2����
sin2���� cos2����
cos2���� .
.
�ⷨ2��
(1)ͬ�ⷨ1.
(2)���Ǻ��ʽΪsin2����cos2(30�㣭��)��sin��cos(30�㣭��)�� .
.
֤�����£�
sin2����cos2(30�㣭��)��sin��cos(30�㣭��)
�� ��
�� ��sin��(cos30��cos����sin30��sin��)
��sin��(cos30��cos����sin30��sin��)
��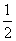 ��
��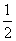 cos2����
cos2����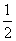 ��
��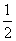 (cos60��cos2����sin60��sin2��)��
(cos60��cos2����sin60��sin2��)�� sin��cos����
sin��cos����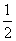 sin2��
sin2��
��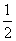 ��
��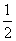 cos2����
cos2����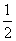 ��
�� cos2����
cos2���� sin2����
sin2���� sin2����
sin2���� (1��cos2��)
(1��cos2��)
��1�� cos2����
cos2���� ��
�� cos2��
cos2��
�� .
.

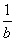 ��
��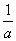 ��1����a��b<1��
��1����a��b<1��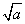 ��
��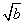 |��1����|a��b|<1��
|��1����|a��b|<1�� ����֪����y��sinx������(0����)�������������ڡ�ABC�У�sinA��sinB��sinC�����ֵΪ______��
����֪����y��sinx������(0����)�������������ڡ�ABC�У�sinA��sinB��sinC�����ֵΪ______��