题目内容
设a,b为正实数,现有下列命题:
①若a2-b2=1,则a-b<1;
②若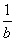 -
-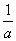 =1,则a-b<1;
=1,则a-b<1;
③若|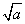 -
-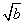 |=1,则|a-b|<1;
|=1,则|a-b|<1;
④若|a3-b3|=1,则|a-b|<1.
其中的真命题有________.(写出所有真命题的编号)
①④
[解析] 本题考查了等式与不等式之间的逻辑关系
对于①,由a2-b2=1,则(a-b)(a+b)=1,
则a-b>0故a>b,又a>0,b>0,则a+b>a-b,若a-b≥1,则a+b>1,则(a+b)(a-b)>1这与已知条件(a-b)(a+b)=1矛盾,故①成立.
对于②,不妨取a=2,b=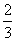 ,则a-b=2-
,则a-b=2-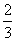 >1,
>1,
故②不正确.
对于③,不妨取a=9,b=4,则|a-b|=5>1,故③不正确,
对于④,由|a3-b3|=1知a≠b,不妨设a>b,若|a-b|≥1,而a≥b+1,又b>0,则a>1,∴a2+ab+b2>1,
由|a3-b3|=|a-b||a2+ab+b2|=|a-b|(a2+ab+b2)
故|a3-b3|>1,这与已知条件矛盾,
解决问题时直接去解不好处理的情况下可选择间接解法例如反证法,对于不正确命题可举一个反例即可.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
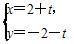 (t为参数)与圆C:
(t为参数)与圆C: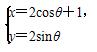 (θ为参数),则直线l的倾斜角及圆心C的直角坐标分别为( )
(θ为参数),则直线l的倾斜角及圆心C的直角坐标分别为( ) ,(1,0) B
,(1,0) B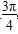 ,(1,0) D.
,(1,0) D.

 D.
D.