题目内容

11．已知点A，B，C，D，E，其中A，E的坐标分别是（-1，2）和（3，-4），则$\overrightarrow{AB}$+$\overrightarrow{DE}$+$\overrightarrow{CD}$+$\overrightarrow{BC}$=（4，-6）．

分析 根据向量的几何意义得到$\overrightarrow{AB}$+$\overrightarrow{DE}$+$\overrightarrow{CD}$+$\overrightarrow{BC}$=$\overline{AE}$=，再根据向量的坐标运算即可求出答案．

解答 解：∵A，E的坐标分别是（-1，2）和（3，-4），
∴$\overline{AE}$=（4，-6），
∴$\overrightarrow{AB}$+$\overrightarrow{DE}$+$\overrightarrow{CD}$+$\overrightarrow{BC}$=$\overline{AE}$=（4，-6）．
故答案为：（4，-6）．

点评 本题考查了向量的几何意义以及向量的坐标运算，属于基础题．

练习册系列答案
相关题目
1．我们要购买一套住房，采用个人住房公积金贷款或个人住房商业性贷款的方式借贷50万元人民币，期限为20年，银行要求每月等额偿还，问每月需要偿还多少资金，贷款利率为6%．
2．已知不等式x2-ax+a-2＞0（a＞2）的解集为（-∞，x1）∪（x2，+∞），则x1+x2+$\frac{1}{{{x}_{1}x}_{2}}$的最小值为4．
19．已知$\overrightarrow{a}$，$\overrightarrow{b}$为两个平面向量，若|$\overrightarrow{a}$|=$\sqrt{2}$|$\overrightarrow{b}$|，$\overrightarrow{a}$$-\overrightarrow{b}$与$\overrightarrow{a}$的夹角为$\frac{π}{6}$，则$\overrightarrow{a}$$-\overrightarrow{b}$与$\overrightarrow{b}$的夹角为（　　）
A．$\frac{π}{4}$B．$\frac{π}{3}$C．$\frac{π}{3}$或$\frac{2π}{3}$D．$\frac{π}{4}$或$\frac{3π}{4}$
6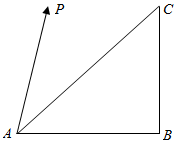．等腰直角△ABC的直角顶点为B，两条直角边长都为1，点P为三角形所在平面内的一点，若$\overrightarrow{AP}$=$λ\overrightarrow{AB}$+$μ\overrightarrow{AC}$，且|$\overrightarrow{AP}$|=1，则λ的取值范围为（　　）
A．[-1，$\sqrt{2}$]B．[-$\sqrt{2}$，$\sqrt{2}$]C．[-$\sqrt{2}$，1]D．[-1，1]
16．有下列3个关系式：
（1）|$\overrightarrow{a}$+$\overrightarrow{b}$|≤|$\overrightarrow{a}$|+|$\overrightarrow{b}$|；
（2）||$\overrightarrow{a}$|-|$\overrightarrow{b}$||≤|$\overrightarrow{a}$|+|$\overrightarrow{b}$|；
（3）|$\overrightarrow{a}$|2=$\overrightarrow{a}$2．其中正确的个数是3．
3．执行如下程序框图，则输出结果为（　　）
A．2B．3C．4D．5
20．执行如图的程序框图，输出S的值为（　　）
A．ln4-ln3B．ln5C．ln5-ln4D．ln4
1．函数y=cos（3x-$\frac{π}{3}$）的最小正周期为$\frac{2π}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网