题目内容
19.已知$\overrightarrow{a}$,$\overrightarrow{b}$为两个平面向量,若|$\overrightarrow{a}$|=$\sqrt{2}$|$\overrightarrow{b}$|,$\overrightarrow{a}$$-\overrightarrow{b}$与$\overrightarrow{a}$的夹角为$\frac{π}{6}$,则$\overrightarrow{a}$$-\overrightarrow{b}$与$\overrightarrow{b}$的夹角为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{π}{4}$或$\frac{3π}{4}$ |
分析 根据向量减法的三角形法则作出三角形,根据正弦定理求出B,则$\overrightarrow{a}$$-\overrightarrow{b}$与$\overrightarrow{b}$的夹角为π-B.
解答 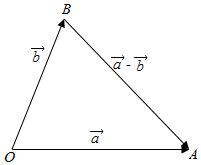 解设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,则$\overrightarrow{BA}=\overrightarrow{a}-\overrightarrow{b}$.
解设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,则$\overrightarrow{BA}=\overrightarrow{a}-\overrightarrow{b}$.
∵$\overrightarrow{a}$$-\overrightarrow{b}$与$\overrightarrow{a}$的夹角为$\frac{π}{6}$,∴A=$\frac{π}{6}$.在△AOB中,由正弦定理得$\frac{OA}{sinB}=\frac{OB}{sinA}$,
∴$\frac{|\overrightarrow{b}|}{\frac{1}{2}}=\frac{|\overrightarrow{a}|}{sinB}$,解得sinB=$\frac{\sqrt{2}}{2}$.
∴B=$\frac{π}{4}$或$\frac{3π}{4}$.
∴$\overrightarrow{a}$$-\overrightarrow{b}$与$\overrightarrow{b}$的夹角为π-B=$\frac{3π}{4}$或$\frac{π}{4}$.
故选:D.
点评 本题考查了平面向量加法的几何意义,正弦定理,向量夹角的计算,属于中档题.

练习册系列答案
相关题目
7.函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(-$\frac{π}{2}$)=( )
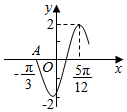
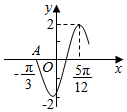
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 1 | D. | -1 |
4.设向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{a}$$+\overrightarrow{b}$$+\overrightarrow{c}$=$\overrightarrow{0}$,且|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,|$\overrightarrow{c}$|=4,则$\overrightarrow{a}$$•\overrightarrow{b}$=( )
| A. | 4 | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |