题目内容
15.已知函数f(x)=$\frac{1}{3}$x3-(a+2)x2+a(a+4)x+5在区间(-1,2)内单调递减,求a的取值范围.分析 解法一:求出导函数,通过f′(x)<0的解为(a,a+4),利用子集关系,转化求解即可.
解法二:求出f′(x),通过f′(x)≤0在区间(-1,2)上恒成立,利用二次函数的性质求解即可.
解答 解法一:f′(x)=x2-2(a+2)x+a(a+4)=(x-a)(x-a-4),…(4分)
f′(x)<0的解为(a,a+4),…(7分)
∵f(x)在区间(-1,2)内单调递减,
∴(-1,2)⊆(a,a+4),…(10分)
由此得a≤-1且a+4≥2,a的范围是[-2,-1].…(12分)
解法二:f′(x)=x2-2(a+2)x+a(a+4),…(2分)
∵f(x)在区间(-1,2)内单调递减,
∴f′(x)≤0在区间(-1,2)上恒成立,…(4分)
∵二次函数f′(x)=x2-2(a+2)x+a(a+4)的开口向上,
∴f′(-1)=a2+6a+5≤0且f′(2)=a2-4≤0 …(10分)
解得a的范围是[-2,-1].…(12分)
点评 本题考查函数的导数的应用,函数恒成立,函数的单调性单调区间的求法,转化思想的应用.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
2.某工厂某产品产量y(千件)与单位成本x(元)满足线性回归方程$\widehat{y}$=75.7-2.13x,则以下说法中正确的是( )
| A. | 产量每增加1000件,单位成本下降2.13元 | |
| B. | 产量每减少1000件,单位成本下降2.13元 | |
| C. | 产量每增加1000件,单位成本上升2130元 | |
| D. | 产量每减少1000件,单位成本上升2130元 |
3.要证明“sin4θ-cos4θ=2sin2θ-1”,过程为:“sin4θ-cos4θ=(sin2θ+cos2θ)(sin2θ-cos2θ)=sin2θ-cos2θ=sin2θ-(1-sin2θ)=2sin2θ-1”,用的证明方法是( )
| A. | 分析法 | B. | 反证法 | C. | 综合法 | D. | 间接证明法 |
10.已知全集U=R,集合A={x|x2-2x-3>0},B={x|2<x<4},那么集合(∁UA)∩B=( )
| A. | {x|-1≤x≤4} | B. | {x|2<x≤3} | C. | {x|2≤x<3} | D. | {x|-1<x<4} |
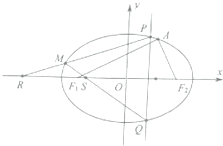 如图,已知椭圆C:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{{b}^{2}}=1(0<b<3)$的左、右焦点分别为F1、F2,椭圆上存在一点A,使得AF1=2AF2,且∠F1AF2=90°
如图,已知椭圆C:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{{b}^{2}}=1(0<b<3)$的左、右焦点分别为F1、F2,椭圆上存在一点A,使得AF1=2AF2,且∠F1AF2=90°