题目内容
20.已知函数g(x)=x2-(2a+1)x+alnx.(1)当a=1时,求函数g(x)的单调增区间;
(2)求函数g(x)在区间[1,e]上的最值.
分析 (1)求出函数的定义域,求出导函数,令导函数大于0,求出x的范围,写出区间形式即得到函数f(x)的单调增区间.
(2)求出导函数,令导函数为0求出根,通过讨论根与区间[1,e]的关系,判断出函数的单调性,求出函数的最小值.
解答 解:f(x)的定义域为x>0
(1)将a=1代入f(x)得f(x)=x2-3x+lnx
所以f′(x)=$\frac{2{x}^{2}-3x+1}{x}$
令f′(x)>0得0<x<$\frac{1}{2}$或x>1
所以函数的单调增区间(0,$\frac{1}{2}$),(1,+∞);
(2)f′(x)=$\frac{2{x}^{2}-(2a+1)+a}{x}$
令f′(x)=0得x=$\frac{1}{2}$(舍)或x=a,
当a≤1时,在区间[1,e]上,f′(x)>0
f(x)在区间[1,e]上的单调递增
所以[f(x)]min=f(1)=-2a;
当1<a<e时,f(x)在[1,a]单调递减,在[a,e]上单调递增
所以[f(x)]min=f(a)=-a2-a+alna;
当a≥e时,f(x)在[1,e]上单调递减
所以[f(x)]min=f(e)=e2-2ae-e+a.
点评 本题考查了导数和函数的单调性和最值关系,熟练掌握利用导数研究函数的单调性、等价转化、二次函数的性质等是解题的关键,属于中档题.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
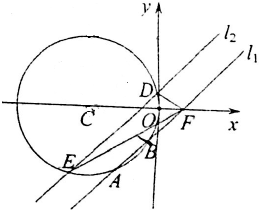 已知直线l1:y=x-1与圆C:(x+a)2+y2=a2(a>0)相交于A、B两点,|AB|=2,直线l2∥l1,直线l2与圆C相交于D、E两点.
已知直线l1:y=x-1与圆C:(x+a)2+y2=a2(a>0)相交于A、B两点,|AB|=2,直线l2∥l1,直线l2与圆C相交于D、E两点.