题目内容
已知函数f（x）=2
+
，若关于x的不等式f（x）≤|m-2|恒成立，则实数m的取值范围是 ．
| x |
| 5-x |
考点：柯西不等式
专题：不等式
分析：由柯西不等式可得（2
+
）2≤（22+12）[（
）2+（
）2]=25，关于x的不等式f（x）≤|m-2|恒成立，等价于|m-2|≥5，即可求出实数m的取值范围．
| x |
| 5-x |
| x |
| 5-x |
解答：
由柯西不等式可得（2
+
）2≤（22+12）[（
）2+（
）2]=25，
当且仅当
=
，即x=4时等号成立；
关于x的不等式f（x）≤|m-2|恒成立，等价于|m-2|≥5，
∴m≥7或m≤-3．
故答案为：（-∞，-3]∪[7，+∞）
| x |
| 5-x |
| x |
| 5-x |
当且仅当
| ||
| 2 |
| ||
| 1 |
关于x的不等式f（x）≤|m-2|恒成立，等价于|m-2|≥5，
∴m≥7或m≤-3．
故答案为：（-∞，-3]∪[7，+∞）
点评：本题考查柯西不等式，考查恒成立问题，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
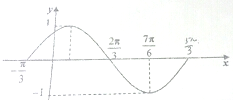已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜