题目内容
13.已知函数f(x)=asin2x+(a+1)cos2x,a∈R,则函数f(x)的最小正周期为π,振幅的最小值为$\frac{\sqrt{2}}{2}$.分析 利用辅助角公式化简,根据周期公式可得最小正周期,根据性质可得振幅的最小值.
解答 解:函数f(x)=asin2x+(a+1)cos2x,a∈R,
化简可得:f(x)=$\sqrt{{a}^{2}+(a+1)^{2}}$sin(2x+θ)=$\sqrt{2(a+\frac{1}{2})^{2}+\frac{1}{2}}$sin(2x+θ),其tanθ=$\frac{1+a}{a}$.
函数f(x)的最小正周期T=$\frac{2π}{2}=π$.
振幅为$\sqrt{2(a+\frac{1}{2})^{2}+\frac{1}{2}}$,
当a=$-\frac{1}{2}$时,可得振幅的最小值$\frac{\sqrt{2}}{2}$.
故答案为:π,$\frac{\sqrt{2}}{2}$.
点评 本题主要考查三角函数的图象和性质,比较基础.

练习册系列答案
相关题目
1.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线方程为$y=\frac{3}{4}x$,则双曲线的离心率为( )
| A. | $\frac{5}{3}$ | B. | $\frac{{\sqrt{21}}}{3}$ | C. | $\frac{5}{4}$ | D. | $\frac{{\sqrt{7}}}{2}$ |
8.把复数z的共轭复数记作$\overline{z}$,若(1+i)z=1-i,i为虚数单位,则$\overline{z}$=( )
| A. | i | B. | -i | C. | 1-i | D. | 1+i |
2.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的渐近线为等边三角形OAB的边OA、OB所在直线,直线AB过焦点,且|AB|=2,则双曲线实轴长为( )
| A. | $\sqrt{3}$ | B. | $3\sqrt{2}$ | C. | $\frac{3}{2}$ | D. | 3 |
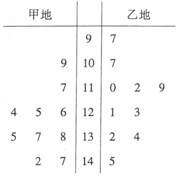 在一次期末模拟测试中,某市教研室在甲、乙两地各抽取了10名学生的数学成绩,得到茎叶图如图所示.
在一次期末模拟测试中,某市教研室在甲、乙两地各抽取了10名学生的数学成绩,得到茎叶图如图所示.


