题目内容
在△ABC中，（a+b+c）（a+b-c）=3ab，2cosAsinB=sinC，则△ABC的形状是（ ）
| A、等边三角形 |
| B、等腰三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
考点：余弦定理,正弦定理
专题：计算题,解三角形
分析：由已知2cosAsinB=sinC=sin（A+B），结合和差角公式可求得A=B，由（a+b+c）（a+b-c）=3ab，可得a2+b2-c2=ab，利用余弦定理可得C，从而可判断三角形的形状．
解答：
解：由三角形的内角和公式可得，2cosAsinB=sinC=sin（A+B）
∴2cosAsinB=sinAcosB+sinBcosA
∴sinAcosB-sinBcosA=0，
∴sin（A-B）=0，∴A=B
∵（a+b+c）（a+b-c）=3ab
∴（a+b）2-c2=3ab
即a2+b2-c2=ab
由余弦定理可得cosC=
=
∵0＜C＜π，∴C=
，∴A=B=C=
故△ABC为等边三角形，
故选：A．
∴2cosAsinB=sinAcosB+sinBcosA
∴sinAcosB-sinBcosA=0，
∴sin（A-B）=0，∴A=B
∵（a+b+c）（a+b-c）=3ab
∴（a+b）2-c2=3ab
即a2+b2-c2=ab
由余弦定理可得cosC=
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
∵0＜C＜π，∴C=
| π |
| 3 |
| π |
| 3 |
故△ABC为等边三角形，
故选：A．
点评：本题考查两角和与差的三角公式及余弦定理解三角形，解题的关键是熟练掌握三角基本公式．
练习册系列答案
相关题目
4名同学参加跳高，跳远和100米跑三项决赛，争夺这三项冠军，则冠军结果有（ ）
| A、34种 | ||
| B、43种 | ||
C、
| ||
D、
|
已知点O是边长为1的等边△ABC的外心，则（
+
）•（
+
）等于（ ）
| OA |
| OB |
| OA |
| OC |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
（A题）下列求导运算正确的是（ ）
A、（x+
| ||||
| B、（3x）′=3xlog3e | ||||
C、（log2x）′=
| ||||
| D、（x2cos x）′=-2xsin x |
已知a＞0且a≠1，f（x）=x2-ax，当x∈（-1，1）时均有f（x）＜
，则实数a的取值范围是（ ）
| 1 |
| 2 |
A、0＜a≤
| ||
B、
| ||
C、
| ||
D、0＜a≤
|
函数y=
+
的定义域是（ ）
| x(x+1) |
| x |
| A、{x|x≥0} |
| B、{x|x≥1} |
| C、{x|x≥0}∪{0} |
| D、{x|0≤x≤1} |
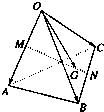（B题）已知空间四边形OABC，M、N分别是对边OA、BC的中点，点G在线段MN上，且| MG |
| GN |
| OG |
| OA |
| OB |
| OC |
A、x=
| ||||||
B、x=
| ||||||
C、x=
| ||||||
D、x=
|