Question

已知a＞0且a≠1，f（x）=x²-a^x，当x∈（-1，1）时均有f（x）＜

1

2

，则实数a的取值范围是（　　）

• A、0＜a≤

  1

  2

  或a≥2
• B、

  1

  4

  ≤a＜1或1＜a≤4
• C、

  1

  2

  ≤a＜1或1＜a≤2
• D、0＜a≤

  1

  4

  或a≥4

Answer 1

考点：函数恒成立问题

专题：综合题,数形结合,函数的性质及应用

分析：由题意可知，a^x＞x²-

1

2

在（-1，1）上恒成立，令y₁=a^x，y₂=x²-

1

2

，结合图象，列出不等式组，解不等式组，求出a的取值范围．

解答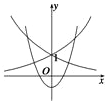： 解：由题意可知，a^x＞x²-

1

2

在（-1，1）上恒成立，令y₁=a^x，y₂=x²-

1

2

，
由图象知：0＜a＜1时a¹≥

1

2

，即

1

2

≤a＜1；
当a＞1时，a^-1≥

1

2

，可得1＜a≤2．
∴

1

2

≤a＜1或1＜a≤2．
故选 C．

点评：本题考查不等式组的解法，体现了数形结合和转化的数学思想．